Hướng dẫn giải nhanh Toán 11 CTST bài 1: Góc lượng giác
Baivan.net sẽ đưa ra lời giải nhanh, ngắn gọn chuẩn xác môn toán 11 bộ sách chân trời sáng tạo bài 1: Góc lượng giác. Đa thức nhiều biến. Học sinh kéo xuống để tham khảo. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt hiệu quả cao trong học tập
1. GÓC LƯỢNG GIÁC
Bài 1: Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA….
Hướng dẫn trả lời:

a)
Thời gian t (giây) | 1 | 2 | 3 | 4 | 5 | 6 |
Góc quay | 60$^{\circ}$ | 120$^{\circ}$ | 180$^{\circ}$ | 240$^{\circ}$ | 300$^{\circ}$ | 360$^{\circ}$ |
b)
Thời gian t (giây) | 1 | 2 | 3 | 4 | 5 | 6 |
Góc quay | -60$^{\circ}$ | -120$^{\circ}$ | -180$^{\circ}$ | -240$^{\circ}$ | -300$^{\circ}$ | -360$^{\circ}$ |
Bài 2: Cho...
Hướng dẫn trả lời:
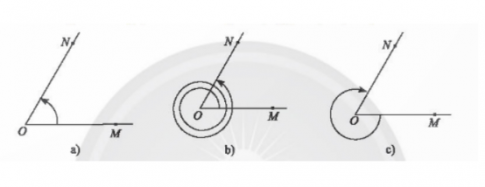
a) Góc lượng giác (OM,ON) = 60$^{\circ}$;
b) Góc lượng giác (OM,ON) = 60$^{\circ}$+2⋅360$^{\circ}$=780$^{\circ}$;
c) Góc lượng giác (OM,ON) = -300$^{\circ}$.
Bài 3: Trong các khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là bao nhiêu độ?
Hướng dẫn trả lời:
Đổi 2 giờ 15 phút = $2\frac{1}{4}$ giờ
Kim phút quay $2\frac{1}{4}$ vòng theo chiều âm nên kim phút đã quét được góc lượng giác là: $\alpha $=-$2\frac{1}{4}$.360$^{\circ}$=-810$^{\circ}$.
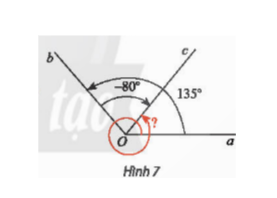
Bài 4: Cho Hình 7….
Hướng dẫn trả lời:
a) Số đo góc lượng giác (Oa,Ob) = 135$^{\circ}$.
Số đo góc lượng giác (Ob,Oc) = -80$^{\circ}$.
aOc=135$^{\circ}$-80$^{\circ}$=55$^{\circ}$. Mà góc lượng giác (Oa,Oc) tương ứng với chuyển động quay theo chiều dương từ Oa đến Oc, sau đó quay thêm 1 vòng.
=> Số đo góc lượng giác (Oa,Oc) = 55$^{\circ}$+360$^{\circ}$=415$^{\circ}$.
b) Như vậy đối với ba góc trong hình, ta có tổng số đo góc lượng giác (Oa,Ob) và (Ob,Oc) chênh lệch với số đo góc lượng giác (Oa,Oc) là một số nguyên lần 360$^{\circ}$.
Bài 5: Trong Hình 8, chiếc quạt có 3 cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox, ON) và (Ox, OP).
Hướng dẫn trả lời:
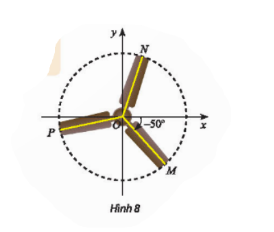
$\widehat{MON}=\widehat{MON}$=$\frac{1}{3}$.360$^{\circ}$=120$^{\circ}$.
Số đo các góc lượng giác (OM,ON) và (OM,OP) lần lượt là 120$^{\circ}$ và -120$^{\circ}$.
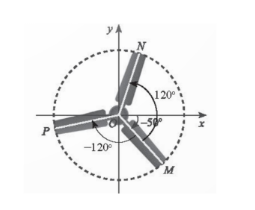
(Ox,ON) =(Ox,OM)+(OM,ON)+k360$^{\circ}$($k\in Z$) =-50$^{\circ}$+120$^{\circ}$+k360$^{\circ}$($k\in Z$) =70$^{\circ}$+k360$^{\circ}$($k\in Z$).
(Ox,OP) =(Ox,OM)+(OM,OP)+k360$^{\circ}$($k\in Z$) =-50$^{\circ}$-120$^{\circ}$+k360$^{\circ}$($k\in Z$) =-170$^{\circ}$+k360$^{\circ}$($k\in Z$).
2. ĐƠN VỊ RADIAN
Bài 1: Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được…
Hướng dẫn trả lời:
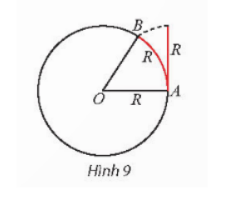
$\widehat{AOB}$ bằng khoảng 57$^{\circ}$.
Bài 2: Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:…
Hướng dẫn trả lời:
Đơn vị độ | 0$^{\circ}$ | 30$^{\circ}$ | 45$^{\circ}$ | 60$^{\circ}$ | 90$^{\circ}$ | 120$^{\circ}$ | 135$^{\circ}$ | 150$^{\circ}$ | 180$^{\circ}$ |
Đơn vị rad | 0 | $\frac{\pi}{6}$rad | $\frac{\pi}{4}$rad | $\frac{\pi}{3}$rad | $\frac{\pi}{2}$rad | $\frac{2\pi}{3}$rad | $\frac{3\pi}{4}$rad | $\frac{5\pi}{6}$rad | $\pi$ rad |
3. ĐƯỜNG TRÒN LƯỢNG GIÁC
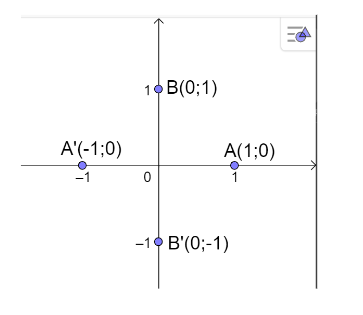
Bài 1: Trong mặt phẳng toạ độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và...
Hướng dẫn trả lời:
a) (OA,OB)=90$^{\circ}$=$\frac{\pi}{2}$+$k2\pi$ rad,$k\in Z$
b) A'(-1;0) và B'(0;-1).
Bài 2: Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo...
Hướng dẫn trả lời:
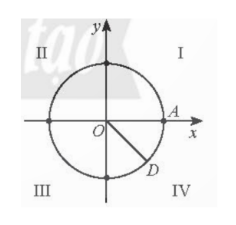
a) -1485$^{\circ}$=-45$^{\circ}$-4.360$^{\circ}$.
Vậy điểm biễu diễn góc lượng giác có số đo -148$^{\circ}$5 là điểm D trên đường tròn lượng giác thuộc góc phần tư thứ IV khi $\widehat{AOD}$=45$^{\circ}$.
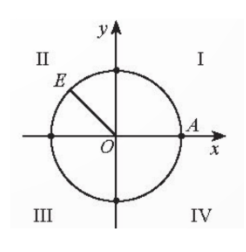
b) $\frac{19\pi}{4}$=$\frac{3\pi}{4}$+$4\pi$
Vậy điểm biểu diễn góc lượng giác có số đo $\frac{19\pi}{4}$ là điểm E trên đường tròn lượng giác thuộc góc phần tư thứ II khi $\widehat{AOE}$=$\frac{3\pi}{4}$.
4. GIẢI BÀI TẬP CUỐI SGK
Bài 1: Đổi số đo của các góc sau đây sang radian:
Hướng dẫn trả lời:
Độ | Radian |
38$^{\circ}$ | $\frac{19\pi}{90}$rad |
-115$^{\circ}$ | - $\frac{23\pi}{36}$rad |
$(\frac{3}{\pi})^{\circ}$ | $\frac{1}{60}$rad |
Bài 2: Đổi số đo của các góc sau đây sang...
Hướng dẫn trả lời:
Radian | Độ |
$\frac{\pi}{12}$rad | 15$^{\circ}$ |
-5=$(\frac{900}{\pi})^{\circ}$ | 286,479 $^{\circ}$ |
$\frac{13\pi}{9}$ | 260$^{\circ}$ |
Bài 3: Biểu diễn các góc lượng giác sau trên đường tròn...
Hướng dẫn trả lời:
a) $\frac{-17\pi}{3}$=$\frac{\pi}{3}$-$3.2\pi$
Vậy điểm biểu diễn góc lượng giác có số đo $\frac{-17\pi}{3}$ là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ I khi $\widehat{AOM}$=$\frac{\pi}{3}$.
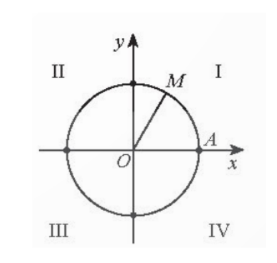
b) $\frac{13\pi}{4}$=$\frac{-3\pi}{4}$-$2.2\pi$
Vậy điễm biểu diễn góc lượng giác có số đo $\frac{13\pi}{4}$ là điểm N trên đường tròn lượng giác thuộc góc phần tư thứ III khi $\widehat{AON}$=$\frac{-3\pi}{4}$.
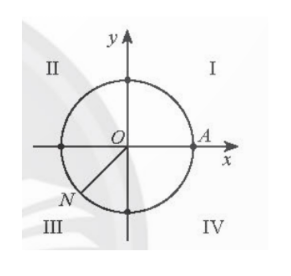
c) -765$^{\circ}$=-45$^{\circ}$-2⋅360$^{\circ}$.
Vậy điểm biểu diễn góc lượng giác có số đo -765$^{\circ}$ là điểm P trên đường tròn lượng giác thuộc góc phần tư thứ IV khi $\widehat{AOP}$=45$^{\circ}$.

Bài 4: Góc lượng...
Hướng dẫn trả lời:
$\frac{31\pi}{7}$=$\frac{3\pi}{7}$+$4\pi$;
$\frac{31\pi}{7}$=$\frac{10\pi}{7}$+$3\pi$;
$\frac{31\pi}{7}$=$\frac{-25\pi}{7}$+$8\pi$.
=> $\frac{31\pi}{7}$ có cùng điểm biểu diễn với góc lượng giác $\frac{3\pi}{7}$ và $\frac{-25\pi}{7}$.
Bài 5: Viết công thức số đo tổng quát của các...
Hướng dẫn trả lời:
(OA,OM)=120$^{\circ}$+k360$^{\circ}$ ($k\in Z$)
(OA,ON)=-75$^{\circ}$+k360$^{\circ}$ ($k\in Z$)
Bài 6: Viết công thức số đo tổng quát của...
Hướng dẫn trả lời:
(OM,ON)=(Ox,OM)+(Ox,ON)+k360$^{\circ}$($k\in Z$)
2.72$^{\circ}$=45$^{\circ}$ +(Ox,ON)+k360$^{\circ}$($k\in Z$)
=> (Ox,ON) = =99$^{\circ}$+k360$^{\circ}$($k\in Z$).
Bài 7: Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số...
Hướng dẫn trả lời:
a)
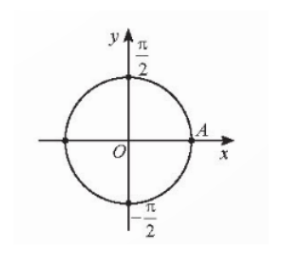
b)
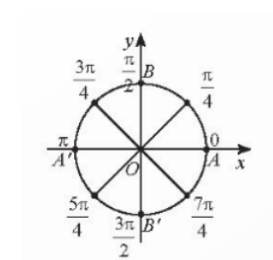
Bài 8: Vị trí các điểm B, C, D trên cánh quạt động cơ...
Hướng dẫn trả lời:
$\frac{\pi}{2}$+k$\frac{2\pi}{3}$($k\in Z$) và $-\frac{\pi}{6}$+k$\frac{2\pi}{3}$($k\in Z$).
Bài 9: Hải li là một đơn vị chiều dài hàng hải, được tính bằng...
Hướng dẫn trả lời:
Ta có $\alpha$=$\frac{1}{60}$.$\frac{\pi}{180}$=$\frac{\pi}{10800}$(rad).
Một hài lí có độ dài là: $\frac{\pi}{10800}$⋅6371≈1,85( km).
