Hướng dẫn giải nhanh Toán 11 CTST bài 1: Giới hạn của dãy số

1. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ

Bài 1: Cho dãy số...

Hướng dẫn trả lời:

a) 

b) $|u_{n}|=\frac{1}{n}$

$|u_{n}|<0,01$ <=> $\frac{1}{n}<0,01$ <=> n>100

$|u_{n}|<0,001$ <=> $\frac{1}{n}<0,001$ <=> n>1000

c) 

Dựa vào trục số, ta thấy được khoảng cách từ $u_{n}$ đến 0 trở nên rất bé khi n trở nên rất lớn.

Bài 2: Tìm các giới hạn sau...

Hướng dẫn trả lời:

a) $\lim{\frac{1}{n^{2}}}=0$ với k nguyên dương bất kì.

b) $\lim{-\frac{3}{4}}^{n}=0$ vì $\lim{q^{n}}=0$, với q là số thực thoả mãn |q|<1, trong trường hợp này $q=\frac{-3}{4}$.

Bài 3: Cho dãy số...

Hướng dẫn trả lời:

a) $v_{n}=u_{n}-2=\frac{2n+1}{n}-2=\frac{1}{n}$

=> $\lim{v_{n}}=\lim{\frac{1}{n}}=0$

b) $u_{1}=\frac{2.1+1}{1}=3$

$u_{2}=\frac{5}{2}$

$u_{3}=\frac{7}{3}$

$u_{4}=\frac{9}{4}$

Bài 4: Tìm các giới hạn sau...

Hướng dẫn trả lời:

a) $\lim{(2+(\frac{2}{3})^{n}-2)}=\lim{(\frac{2}{3})^{n}}=0$ 

=> $\lim{(2+(\frac{2}{3})^{n})}=2$

b) $\lim{(\frac{1-4n}{n}-(-4))}=\lim{\frac{1}{n}}=0$

=> $\lim{(\frac{1-4n}{n})}=-4$.

2. CÁC PHÉP TOÁN VỀ GIỚI HẠN HỮU HẠN CỦA DÃY SỐ

Bài 1: Ở trên ta đã biết...

Hướng dẫn trả lời:

a) $\lim{3}=3$ (3 là hằng số)

$\lim{\frac{1}{n^{2}}}=0$

b) $\lim{(3+\frac{1}{n^{2}})}=\lim{3}+\lim{\frac{1}{n^{2}}} = 3$

Bài 2: Tìm các giới hạn sau...

Hướng dẫn trả lời:

a) $\lim{\frac{2n^{2}+3n}{n^{2}-1}}$

= $\lim{\frac{2+3.\frac{1}{n}}{1-\frac{1}{n^{2}}}}$

= $\frac{\lim{(2+3.\frac{1}{n})}}{\lim{(1-\frac{1}{n^{2}})}}$

= $\frac{\lim{2}+3\lim{\frac{1}{n}}}{\lim{1}-\lim{\frac{1}{n^{2}}}}$

= 2

b) $\lim{\frac{\sqrt{4n^{2}+3}}{n}}$

= $\lim{\sqrt{\frac{4n^{2}+3}{n^{2}}}}$

= $\sqrt{\lim{(4+\frac{3}{n^{2}})}}$

= $\sqrt{\lim{4}+3.\lim{\frac{1}{n^{2}}}}$ = 2

3. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN

Bài 1: Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông, rồi tô màu một nửa còn lại, và cứ tiếp tục như...

Hướng dẫn trả lời:

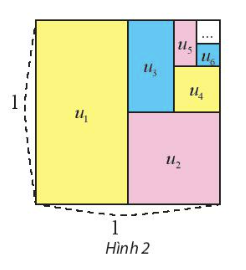
a) ($u_{k}$) là cấp số nhân với $u_{1}=\frac{1}{2}$, $q =\frac{1}{2}$

$u_{k}=u_{1}.q^{k-1}=\frac{1}{2^{k}}$ 

b) $S_{n}=\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+…+\frac{1}{2^{n}}$

= $\frac{1}{2}.\frac{1-\frac{1}{2^{n}}}{1-\frac{1}{2}}=1-\frac{1}{2^{n}}$

c) $\lim{S_{n}}=\lim{(1-\frac{1}{2^{n}})}=\lim{1}-\lim{\frac{1}{2^{n}}}=1$ 

Vậy giới hạn này bằng diện tích của hình vuông ban đầu.

Bài 2: Tính tổng của cấp số nhân lùi vô hạn...

Hướng dẫn trả lời:

Tổng của cấp số nhân lùi vô hạn có $u_{1}=1$ và $q=\frac{1}{3}$

S = $1+\frac{1}{3}+(\frac{1}{3})^{2}+…+(\frac{1}{3})^{n}+…1+\frac{1}{3}+(\frac{1}{3})^{2}+…+(\frac{1}{3})^{n}+… $

= $\frac{1}{1-\frac{1}{3}}=\frac{3}{2}$.

Bài 3: Từ tờ giấy, cắt một hình tròn bán kính R (cm) như Hình 3a...

Hướng dẫn trả lời:

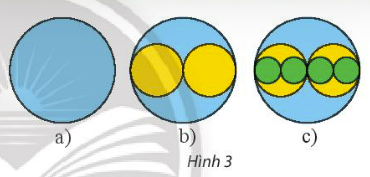
S = $\pi R^{2}+2\pi (\frac{R}{2})^{2}+4\pi (\frac{R}{4})^{2}+…+2^{n}\pi (\frac{R}{2^{n}})^{2}+...$ 

= $\pi R^{2}(1+\frac{1}{2}+\frac{1}{2^{2}}+…+\frac{1}{2^{n}}+…)$ 

= $\pi R^{2}\frac{1}{1-\frac{1}{2}}$

= $2\pi R^{2}$ 

4. GIỚI HẠN VÔ CỰC

Bài 1: Dựng một dãy hình vuông bằng cách ghép từ các hình vuông...

Hướng dẫn trả lời:

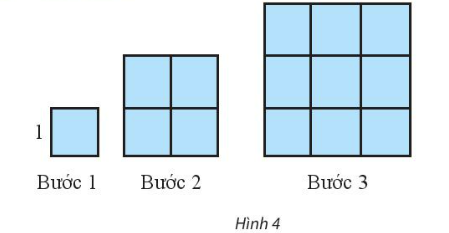
a) Ta có: $u_{1}=1^{2}$; $u_{2}=2^{2}$; $u_{3}=3^{2}$

=> Phương thức tổng quát: $u_{n}=n^{2}$

$u_{n}=n^{2}>10000=100^{2}$ <=> n>100;

$u_{n}=n^{2}>1000000=1000^{2}$ <=> n>1000.

b) $u_{n}>S$ <=>  $n^{2}>S$ <=> $n>\sqrt{S}$. 

Vậy với những số tự nhiên $n>\sqrt{S}$ thì $u_{n}>S$.

5. GIẢI BÀI TẬP CUỐI SGK

Bài 1: Tìm các giới hạn sau...

Hướng dẫn trả lời:

a) $\lim{\frac{-2n+1}{n}}=\lim{(-2+\frac{1}{n})}=\lim{(-2)}+\lim{\frac{1}{n}}=-2$

b) $\lim{\frac{\sqrt{16n^{2}-2}}{n}}$

= $\lim{\sqrt{\frac{16n^{2}-2}{n^{2}}}}=\lim{\sqrt{16-\frac{2}{n^{2}}}}$

= $\sqrt{\lim{(16-\frac{2}{n^{2}})}}$

= $\sqrt{\lim{16}-2\lim{\frac{1}{n^{2}}}}$ =4 

c) $\lim{\frac{4}{2n+1}}$

= $\lim{\frac{\frac{4}{n}}{\frac{2n+1}{n}}}$

= $\frac{4.\lim{\frac{1}{n}}}{\lim{2}+\lim{\frac{1}{n}}}$=0

d) $\lim{\frac{n^{2}-2n+3}{2n^{2}}}$

= $\lim{(\frac{1}{2}-\frac{1}{n}+\frac{3}{2n^{2}})}$

= $\lim{\frac{1}{2}}-\lim{\frac{1}{n}}+\frac{3}{2}\lim{\frac{1}{n^{2}}}$

= $\frac{1}{2}$.

Bài 2: Tính tổng của các cấp số nhân lùi vô hạn sau...

Hướng dẫn trả lời:

a) Đây là tổng của cấp số nhân lùi vô hạn có $u_{1}=-\frac{1}{2}$ và $q=-\frac{1}{2}$

$-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+…+(-\frac{1}{2})^{n}+…$

= $-\frac{1}{2}.\frac{1}{1-(-\frac{1}{2})}$

= $-\frac{1}{3}$ 

b) Đây là tổng của cấp số nhân lùi vô hạn có $u_{1}=\frac{1}{4}$ và $q=\frac{1}{4}$

$\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+…+(\frac{1}{4})^{n}+…$

= $\frac{1}{4}.\frac{1}{1-\frac{1}{4}}$

= $\frac{1}{3}$ 

Bài 3: Viết số thập phân vô hạn tuần hoàn 0,444... dưới dạng một phân số

Hướng dẫn trả lời:

0,444… = 0,4+0,04+0,004+… 

= $0,4(1+\frac{1}{10}+\frac{1}{10^{2}}+… )$

= $0,4.\frac{1}{1-\frac{1}{10}}$

= $0,4.\frac{10}{9}$

= $\frac{4}{9}$

Bài 4: Từ hình vuông đầu tiên có cạnh bằng...

Hướng dẫn trả lời:

a) Hình vuông thứ n có độ dài cạnh a => Hình vuông thứ n+1 có độ dài cạnh

$\frac{a\sqrt{2}}{2}=\frac{a}{\sqrt{2}}$. 

Từ đó, hình vuông lần lượt có độ dài cạnh là: 1; $\frac{1}{\sqrt{2}}$; $\frac{1}{(\sqrt{2})^{2}}$; $\frac{1}{(\sqrt{2})^{3}}$;…; $\frac{1}{(\sqrt{2})^{n}}$;…. 

=> Ta có công thức tổng quát: $u_{n}=\frac{1}{(\sqrt{2})^{n-1}}$

Diện tích của hình vuông thứ n là $a_{n}=(u_{n})^{2}=\frac{1}{2^{n-1}}$

=> $S_{n}=1+\frac{1}{2}+\frac{1}{2^{2}}+…+\frac{1}{2^{n-1}}$

= $1.\frac{1-\frac{1}{2^{n}}}{1-\frac{1}{2}}$

= $2(1-\frac{1}{2^{n}})$

$\lim{S_{n}}=\lim{(2(1-\frac{1}{2^{n}}))}=2(1-\lim{(\frac{1}{2})^{n}}=2$

b) Chu vi của hình vuông thứ n là 

$p_{n}=4u_{n}=\frac{4}{(\sqrt{2})^{n-1}}$

=> $Q_{n}=4[1+\frac{1}{\sqrt{2}}+\frac{1}{(\sqrt{2})^{2}}+\frac{1}{(\sqrt{2})^{3}}+…+\frac{1}{(\sqrt{2})^{n-1}}]$

= $4.\frac{1-\frac{1}{(\sqrt{2})^{n}}}{1-\frac{1}{\sqrt{2}}}$

$\lim{Q_{n}}=\frac{4}{1-\frac{1}{\sqrt{2}}}$

= $\frac{4\sqrt{2}}{\sqrt{2}-1}=4\sqrt{2}(\sqrt{2}+1)=4(2+\sqrt{2})$

Bài 5: Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau...

Hướng dẫn trả lời:

a) $S_{n}=5^{n}.(\frac{1}{3^{n}})^{2}=5^{n}.\frac{1}{9^{n}}=(\frac{5}{9})^{n}$, n=1,2,3,… 

=> $\lim{S_{n}}=\lim{(\frac{5}{9})^{n}}=0$

b) $p_{n}=5^{n}.4.\frac{1}{3^{n}}=4(\frac{5}{3})^{n}$, n=1,2,3,…

Vì $\lim{\frac{1}{4(\frac{5}{3})^{n}}=\frac{1}{4}\lim{(\frac{3}{5})^{n}}}=0$ và $4(\frac{5}{3})^{n}>0$ $\forall$ n

=> $\lim{ p_{n}}=\lim{(4(\frac{5}{3})^{n})}$ = $+\infty$