Hướng dẫn giải nhanh Toán 11 CTST bài 2: Giá trị lượng giác của một góc lượng giác

1. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC

Bài 1: Trong Hình 1, M và N lần lượt là các điểm biểu diễn của các góc lượng giác...

Hướng dẫn trả lời:

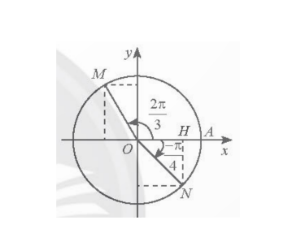
Ta có $\widehat{xOM}=\frac{2\pi}{3}=120^{\circ}$. 

Do đó, $x_{M}=cos120^{\circ}=\frac{1}{2}$, $y_{M}=sin120^{\circ}=\frac{\sqrt{3}}{2}$

=> $M(-\frac{1}{2};\frac{\sqrt{3}}{2})$

Ta có $\widehat{xON}=\frac{\pi}{4}=45^{\circ}$. 

=>$\triangle OHN$ là tam giác vuông cân với cạnh huyền ON=1.

Ta có : $OH^{2}+NH^{2}=ON^{2}$

<=> $2OH^{2}=1$

=> $OH=NH=\frac{\sqrt{2}}{2}$

Vì N nằm trong góc phần tư thứ IV, nên $x_{N}=OH=\frac{\sqrt{2}}{2}$ và $y_{N}=-NH=-\frac{\sqrt{2}}{2}$. 

Do đó N($\frac{\sqrt{2}}{2}$;-\frac{\sqrt{2}}{2}$).

Bài 2: Tính sin(-23) và tan(495)

Hướng dẫn trả lời:

$sin(-\frac{2\pi}{3})=-sin(\frac{2\pi}{3})=-\frac{\sqrt{3}}{2}$
Vì 495$^{\circ}=135^{\circ}+360^{\circ} nên tan⁡495^{\circ}=tan⁡135^{\circ}=\frac{sin135^{\circ}}{cos135^{\circ}}=-1$

2. TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẰNG MÁY TÍNH CẦM TAY

Bài 1: Sử dụng máy tính cầm tay để tính cos75 và tan(-196).

Hướng dẫn trả lời:

$cos75^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}\approx 0,259$

$tantan(\frac{-19\pi}{6})=-\frac{\sqrt{3}}{3}\approx -0,577$

3. HỆ THỨC CƠ BẢN GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC

Bài 1:

a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác...

Hướng dẫn trả lời:

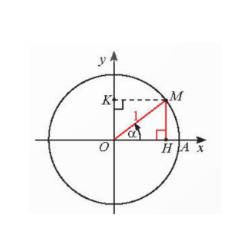
a) $\triangle OMH$ vuông tại H, ta có $O=cos⁡\alpha$, $MH=sin⁡ \alpha$và OM=1.

$OH^{2}+MH^{2}=OM^{2}$ (định lí Pythagore)

⬄ $cos^{2}\alpha⁡+sin^{2}\alpha⁡=1$.

b) Chia cả hai vế cho $cos^{2}\alpha$⁡($cos\alpha $⁡≠0), ta được $1+tan^{2}\alpha⁡=\frac{1}{cos^{2}\alpha}$.

c) Chia cả hai vế cho $sin^{2}\alpha$⁡($cos\alpha$⁡≠0), ta được $cot^{2}\alpha⁡+1=\frac{1}{sin^{2}\alpha}$.

Bài 2: Cho $tan\alpha $...

Hướng dẫn trả lời:

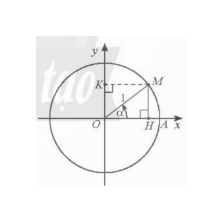
Ta có:  $\frac{1}{cos^{2}\alpha}⁡=1+tan^{2}\alpha=1+(\frac{2}{3})^{2}=\frac{13}{9}$.

=> $cos^{2}\alpha=\frac{9}{13}$.

Do$ \pi<\alpha<\frac{3\pi}{2}$ nên $cos \alpha <0$ => $cos \alpha=-\frac{3\sqrt{3}}{13}$

$tantan \alpha=\frac{sinsin\alpha}{coscos\alpha}$=> $sin\alpha=tan\alpha.cos\alpha=\frac{2}{3}.(-\frac{3\sqrt{3}}{13})=-\frac{2\sqrt{3}}{13}$

4. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC LƯỢNG GIÁC CÓ LIÊN QUAN ĐẶC BIỆT

Bài 1:

a) Biểu diễn...

Hướng dẫn trả lời:

a) cos⁡638$^{\circ}$=cos(⁡-82$^{\circ}$+2⋅360$^{\circ}$)=cos⁡82$^{\circ}$=sin(⁡90$^{\circ}$-82$^{\circ}$)=sin⁡8$^{\circ}$;

b) $cot\frac{19\pi}{5}=cot(4\pi-\frac{\pi}{5})=-cot\frac{\pi}{5}$

Bài 2: Trong Hình 11, vị trí cabin...

Hướng dẫn trả lời:

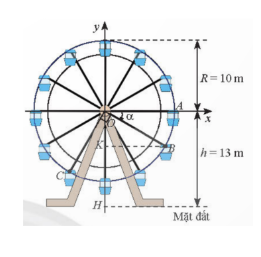
a) Tung độ của H và K lần lượt là $y_{H}=-13$ và $y_{K}=OB⋅sin⁡(OA,OB)=10sin⁡\alpha$.

=> $KH=y_{K}-y_{H}=10sin\alpha⁡+13$.

Với $\alpha=-30^{\circ}$ thì $KH=13+10sin⁡(-30^{\circ})=8$ (m).

b) KH=4 <=>$ 13+10sin\alpha⁡=4 $

=> $sin\alpha⁡=-\frac{9}{10}$ 

=> $\alpha$ thuộc góc phần tư thứ III hoặc góc phần tư thứ IV. Khi đó độ cao của cabin C là $h=13+10sin⁡(OA,OC)=13+10sin(⁡\alpha-90^{\circ})=13-10cos\alpha⁡$.

TH1: thuộc góc phần tư thứ III nên $cos\alpha⁡<0$.

$cos⁡\alpha=-\sqrt{1-sin^{2}\alpha}=\frac{-\sqrt{19}}{10}$.

=> $h=13-10.\frac{\sqrt{-19}}{10}\approx 17,36$( m).

TH2: thuộc góc phần tư thứ IV nên $cos⁡\alpha>0$. 

$cos⁡\alpha=\sqrt{1-sin^{2}\alpha}=\frac{\sqrt{19}}{10}$

=> $h=13-10.\frac{\sqrt{-19}}{10}\approx 8,64$( m).

5. GIẢI BÀI TẬP CUỐI SGK

Bài 1: Các đẳng thức sau có thể đồng thời xảy ra...

Hướng dẫn trả lời:

a) Có. 

Vì $(\frac{3}{5})^{2}+(\frac{-4}{5})^{2}=1$ => tồn tại điểm $M(\frac{3}{5};\frac{-4}{5})$ trên đường tròn lượng giác 

b) Không. 

Vì $sin\alpha=\frac{1}{3}$ và $cot\alpha=\frac{1}{2}$ không thoả mãn đằng thức $\frac{1}{sin^{2}\alpha}=cot^{2}\alpha +1$

c) Có. 

Chọn là một góc có $tan⁡\alpha=3$ thì $cot\alpha=\frac{1}{tan\alpha}=\frac{1}{3}$ nên thoả mãn điều kiện.

Bài 2: Cho $cos\alpha = -\frac{5}{13}$...

Hướng dẫn trả lời:

$sin(-\frac{15\pi}{2}-\alpha)-cos(13\pi+\alpha)$

=$sin(-8\pi+\frac{\pi}{2}+\pi+\alpha)$

=$cos\alpha+cos\alpha=2cos\alpha=-\frac{10}{13}$

Bài 3: Tính các giá trị lượng giác...

Hướng dẫn trả lời:

a) $cos\alpha=-\frac{12}{13}$; $tan\alpha=-\frac{5}{12}$; $cot\alpha=-\frac{12}{5}$;

b) $sin\alpha=\frac{\sqrt{21}}{5}$; $tan\alpha=\frac{\sqrt{21}}{2}$; $cot\alpha=\frac{2\sqrt{21}}{21}$

c) $sin\alpha=-\frac{\sqrt{3}}{2}$; $cos\alpha=-\frac{1}{2}$; $cot\alpha=\frac{\sqrt{3}}{3}$

d) $sin\alpha=-\frac{2\sqrt{5}}{5}$; $cos\alpha=\frac{\sqrt{5}}{5}$; $tan\alpha=-2$

Bài 4: Biểu diễn các...

Hướng dẫn trả lời:

a) $cos\frac{31\pi}{6}=cos(5\pi+\frac{\pi}{6})=cos(\pi+\frac{\pi}{6})=-cos\frac{\pi}{6}=-\frac{\sqrt{3}}{2}$

b) $sin\frac{129\pi}{4}=sin(32\pi+\frac{\pi}{4})=sin\frac{\pi}{4}=\frac{\sqrt{2}}{2}$

c) $tan⁡1020^{\circ}=tan⁡3.360^{\circ}-60^{\circ}=tan⁡-60^{\circ}=-\sqrt{2}$.

Bài 5: Chứng minh các đẳng thức lượng giác sau...

Hướng dẫn trả lời:

a) $\alpha-\alpha=(\alpha+\alpha)(\alpha-\alpha)=sin^{2}\alpha-cos^{2}\alpha=(1-cos^{2}\alpha)-cos^{2}\alpha=1-2cos^{2}\alpha$ (đpcm)

b) $tan\alpha+cot\alpha=\frac{sin\alpha}{cos\alpha}+\frac{cos\alpha}{sin\alpha}=\frac{sin^{2}\alpha+cos^{2}\alpha}{sin\alpha cos\alpha}=\frac{1}{sin\alpha cos\alpha}$ (đpcm)

Bài 6: Rút gọn các biểu thức sau...

Hướng dẫn trả lời:

a) $\frac{1}{tan\alpha+1}+\frac{1}{cot\alpha+1}=\frac{cot\alpha+tan\alpha+2}{cot\alpha+tan\alpha+2}=1$

b) $cos(\frac{\pi}{2}-\alpha)-sin(\pi+\alpha)=sin\alpha+sin\alpha=2sin\alpha$

c) $sin(\alpha-\frac{\pi}{2})+cos(-\alpha+6\pi)-tan(\alpha+\pi)cot(3\pi-\alpha)$

=$-sin(\frac{\pi}{2}-\alpha)+cos(3.2\pi-\alpha)-tan(\alpha+\pi).cot(2\pi+\pi-\alpha)$

=$-sin\alpha+cos\alpha+tan\alpha.cot\alpha$

=$sin\alpha+cos\alpha$

Bài 7: Thanh OM quay...

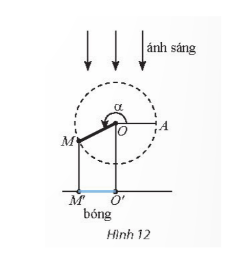
Hướng dẫn trả lời:

Ta có $\alpha=(3\frac{1}{10}).2\pi=\frac{31\pi}{5}$(rad).

Độ dài bóng O'M' của là: 

$O'M'=|OMcos\alpha⁡|=|15cos\frac{31\pi}{5}| \approx 8,8$ (cm). 

Bài 8: Khi xe đạp di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ...

Hướng dẫn trả lời:

Khoảng cách từ van đến mặt đất là $h=R+Rsin\alpha⁡=R(1+sin\alpha⁡)$.

Vì bánh xe quay cùng chiều kim đồng hồ (chiều âm) với tốc góc là 11rad/s, nên sau 1 phút =60 giây, ta có $\alpha=(-11).60=-660$ (rad).

Do đó, khoảng cách từ van đến mặt đất là:

h=58[1+sin⁡(-660)]≈42,8 (cm).