Tải giáo án Powerpoint Toán 9 phần hình học cánh diều 2024 mới nhất

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC MÔN TOÁN!

KHỞI ĐỘNG

Hình 28 minh họa một máy bay cất cánh từ vị trí  trên đường băng của sân bay và bay theo đường thẳng  tạo với phương nằm ngang  một góc là . Sau 5 giây, máy bay ở độ cao .

Có thể tính khoảng cách  bằng cách nào?

CHƯƠNG IV. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG

Bài 3. ỨNG DỤNG CỦA TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN

NỘI DUNG BÀI HỌC

ƯỚC LƯỢNG KHOẢNG CÁCH

ƯỚC LƯỢNG CHIỀU CAO

1. ƯỚC LƯỢNG KHOẢNG CÁCH

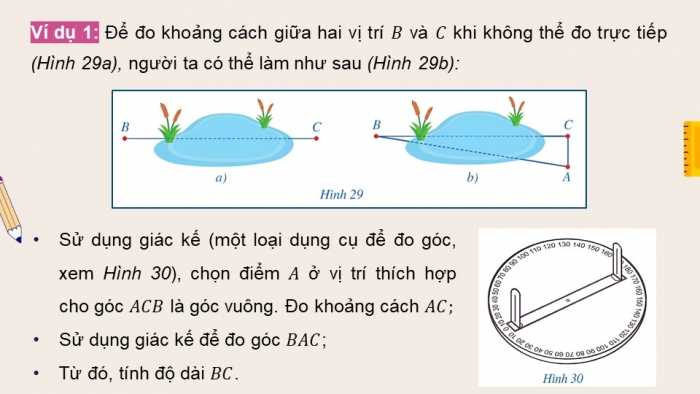
Ví dụ 1: Để đo khoảng cách giữa hai vị trí  và  khi không thể đo trực tiếp (Hình 29a), người ta có thể làm như sau (Hình 29b):

• Sử dụng giác kế (một loại dụng cụ để đo góc, xem Hình 30), chọn điểm ở vị trí thích hợp cho góc  là góc vuông. Đo khoảng cách
• Sử dụng giác kế để đo góc ;
• Từ đó, tính độ dài .

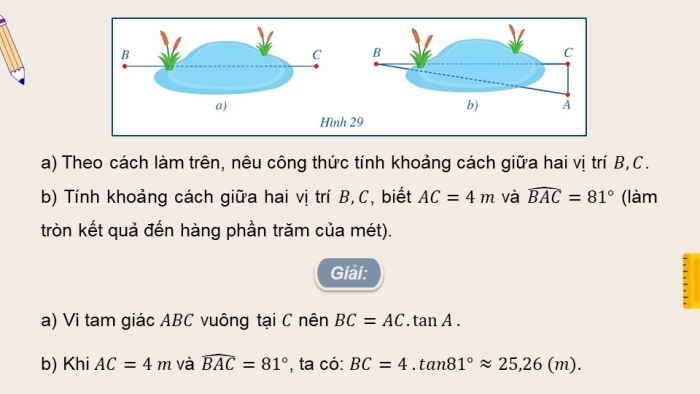
1. a) Theo cách làm trên, nêu công thức tính khoảng cách giữa hai vị trí .
2. b) Tính khoảng cách giữa hai vị trí , biết và (làm tròn kết quả đến hàng phần trăm của mét).

Giải:

1. a) Vì tam giác vuông tại nên
2. b) Khi và , ta có:

Ví dụ 2: Năm 1990, tháp nghiêng ở thành phố Pisa (Italia) bắt đầu quá trình trùng tu nhằm giảm độ nghiêng của tháp. Sau 10 năm trùng tu, vào năm 2001, các kĩ sư đã thành công trong việc đưa độ nghiêng của tháp chỉ còn khoảng 4° (Nguồn: https://en.wikipedia.org/wiki/Leaning_Tower_ of_Pisa). Giả sử một người đứng trên tháp (tại vị trí ), cách mặt đất một khoảng là , thả một vật rơi xuống đất (Hình 31). Tính khoảng cách từ vị trí chạm đất (vị trí ) đó đến chân tháp (vị trí ) (làm tròn kết quả đến hàng phần trăm của mét).

Giải:

Xét tam giác  vuông tại , ta có:

Vậy khoảng cách từ vị trí chạm đất đến chân tháp là khoảng

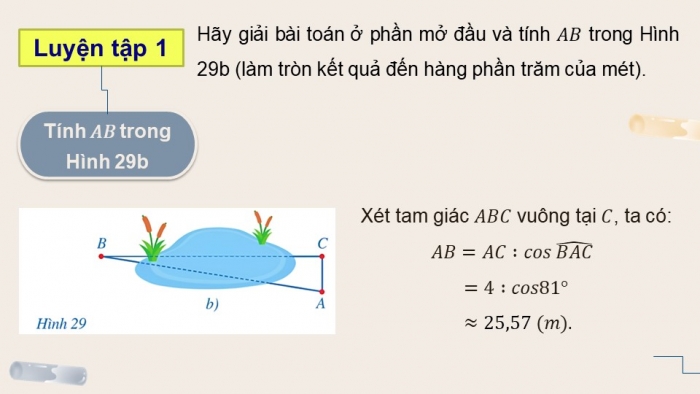
Luyện tập 1

Hãy giải bài toán ở phần mở đầu và tính  trong Hình 29b (làm tròn kết quả đến hàng phần trăm của mét).

Giải bài toán ở phần mở đầu

Xét tam giác  vuông tại , ta có:

Xét tam giác  vuông tại , ta có:

1. ƯỚC LƯỢNG CHIỀU CAO

Ví dụ 3: Để ước lượng chiều cao của một tháp mà không cần lên đỉnh tháp, người ta sử dụng giác kế, thước cuộn, máy tính cầm tay. Chẳng hạn, ở Hình 32, để đo chiều cao  của tháp, người ta đặt giác kế tại một điểm quan sát cách chân tháp một khoảng         , trong đó chiều cao của điểm đặt giác kế là . Quay thanh giác kế sao cho khi ngắm thanh này ta nhìn thấy đỉnh  của tháp, đọc trên giác kế số đo  của góc . Tính chiều cao của tháp, biết (làm tròn kết quả đến hàng phần trăm của mét).

Giải:

Vì tam giác  vuông tại  nên

Vậy chiều cao của tháp khoảng:

Ví dụ 4: Trong lần đến tham quan tháp Eiffel (ở Thủ đô Paris, Pháp), bạn Vân muốn ước tính độ cao của tháp. Sau khi quan sát, bạn Vân đã minh hoạ lại kết quả đo đạc ở Hình 34. Em hãy giúp bạn Vân tính độ cao  của tháp Eiffel theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).

Tháp Eiffel

Giải:

Xét tam giác  vuông tại , ta có:

Xét tam giác  vuông tại , ta có:

Do nên

 hay

Vậy tháp Eiffel có độ cao khoảng

Luyện tập 2

Mặt cắt đứng của khung thép có dạng tam giác cân  với  (Hình 33). Tính độ dài đoạn thẳng  (làm tròn kết quả đến hàng phần mười của mét).

Giải:

Gọi  là trung điểm của  suy ra  là trung tuyến cũng là đường cao của .

Xét  vuông tại  có:

Suy ra .

LUYỆN TẬP

Câu 1. Một chiếc thang dài . Cần đặt chân thang cách tường một khoảng bằng bao nhiêu để nó tạo với phương nằm ngang của mặt đất một góc an toàn  (Làm tròn đến chữ số thập phân thứ hai)

……………….