Tải giáo án Powerpoint Toán 9 phần hình học kết nối tri thức 2024 mới nhất

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC MÔN TOÁN!

KHỞI ĐỘNG

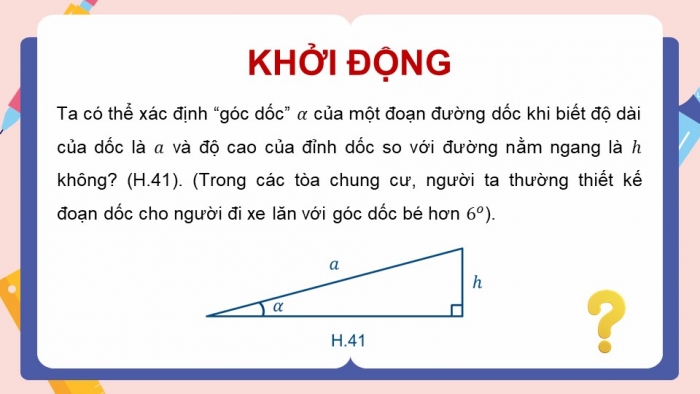
Ta có thể xác định “góc dốc”  của một đoạn đường dốc khi biết độ dài của dốc là  và độ cao của đỉnh dốc so với đường nằm ngang là  không? (H.41). (Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn ).

CHƯƠNG IV. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG

BÀI 11. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN

NỘI DUNG BÀI HỌC

Khái niệm tỉ số lượng giác của một góc nhọn

Tỉ số lượng giác của hai góc phụ nhau

Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn

01 KHÁI NIỆM TỈ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN

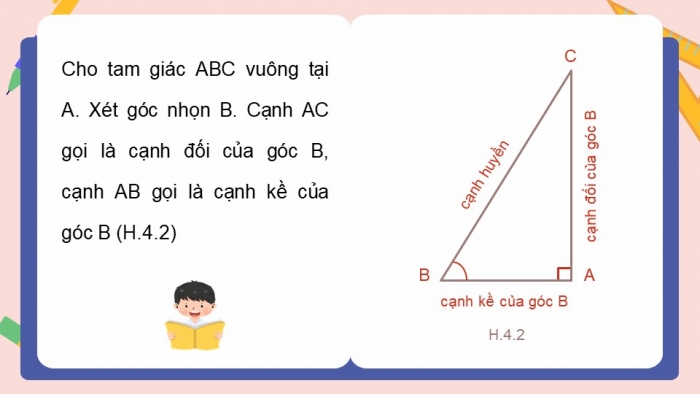
Cho tam giác ABC vuông tại A. Xét góc nhọn B. Cạnh AC gọi là cạnh đối của góc B, cạnh AB gọi là cạnh kề của góc B (H.4.2)

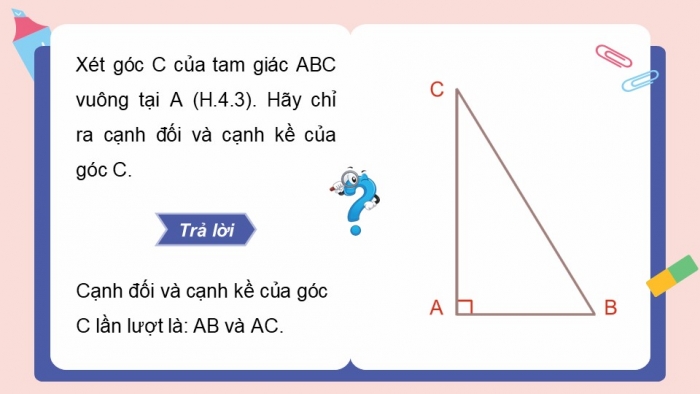
Xét góc C của tam giác ABC vuông tại A (H.4.3). Hãy chỉ ra cạnh đối và cạnh kề của góc C.

Trả lời

Cạnh đối và cạnh kề của góc  C lần lượt là: AB và AC.

Khái niệm sin, côsin, tang, côtang của góc nhọn

• HĐ1. Cho tam giác vuông tại  và tam giác vuông tại  có  Chứng minh rằng:

∽

Giải

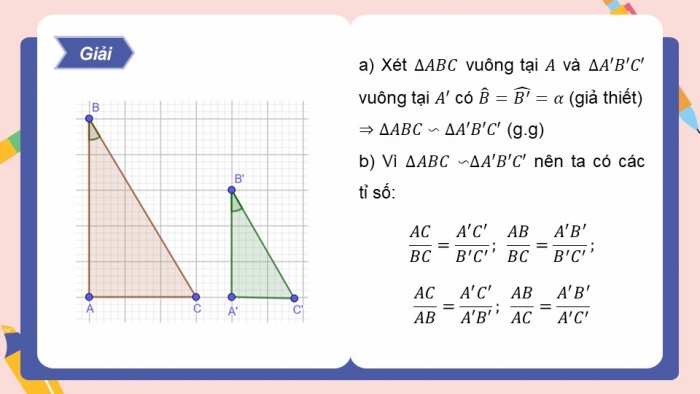
1. a) Xét vuông tại và  vuông tại  có  (giả thiết)

∽  (g.g)

1. b) Vì ∽nên ta có các    tỉ số:

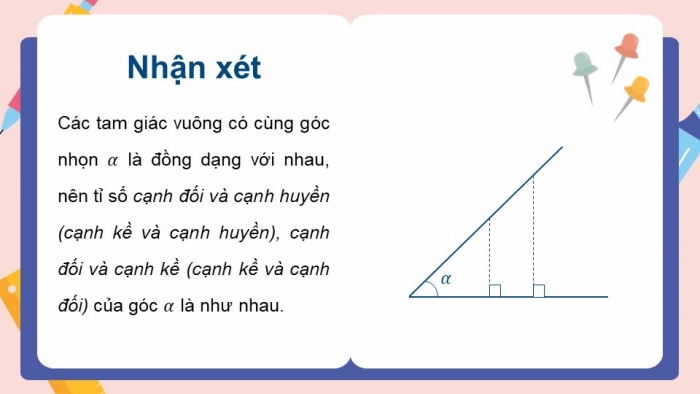
Nhận xét

Các tam giác vuông có cùng góc nhọn  là đồng dạng với nhau, nên tỉ số cạnh đối và cạnh huyền (cạnh kề và cạnh huyền), cạnh đối và cạnh kề (cạnh kề và cạnh đối) của góc  là như nhau.

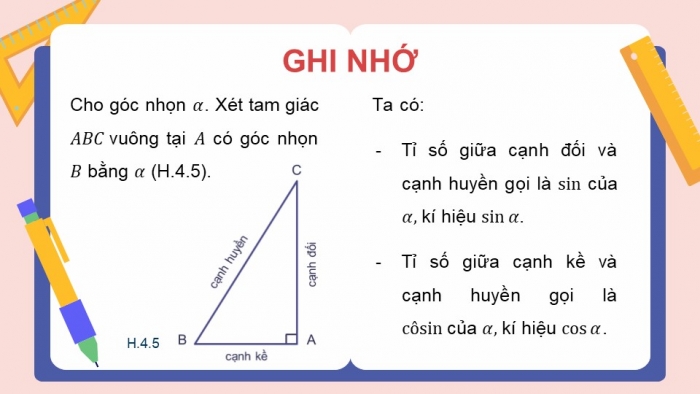
GHI NHỚ

Cho góc nhọn . Xét tam giác vuông tại  có góc nhọn  bằng  (H.4.5).

Ta có:

• Tỉ số giữa cạnh đối và cạnh huyền gọi là của kí hiệu .
• Tỉ số giữa cạnh kề và cạnh huyền gọi là của kí hiệu .
• Tỉ số giữa cạnh đối và cạnh kề của góc gọi là  của kí hiệu .
• Tỉ số giữa cạnh kề và cạnh đối của góc gọi là  của kí hiệu .

Chú ý

 gọi là các tỉ số lượng giác của góc nhọn .

• và  của góc nhọn luôn dương và bé hơn 1 vì trong tam giác vuông, cạnh huyền dài nhất.

Ví dụ 1: Cho tam giác  vuông tại , có  (H.4.6)

Hãy tính các tỉ số lượng giác  với .

Giải

Xét  vuông tại ,  

Theo định lí Pythagore, ta có

Nên

Theo định nghĩa của tỉ số lượng giác , ta có:

Luyện tập 1

Cho tam giác  vuông tại  có  Hãy tính các tỉ số lượng giác của góc .

Giải

Áp dụng định lí Pythagore vào  vuông tại  

Xét  vuông tại  có:

Giá trị lượng giác sin, côsin, tang, côtang của các góc

• HĐ2. Cho tam giác vuông cân tại  và tam giác  

Giải

1. a) Áp dụng định lí Pythagore vào vuông tại :

• HĐ3. Xét tam giác đều có cạnh bằng

1. a) Tính đường cao của tam giác  
2. b) Tính
3. c) Tính

Giải

1. a) Áp dụng định lí Pythagore vào vuông tại có:
2. b)
3. c)

Bảng tỉ số lượng giác của các góc đặc biệt

Ví dụ 2: Cho tam giác  vuông tại , có  và  (H.4.8). Tính các cạnh  theo

Giải

Luyện tập 2

Cho tam giác  vuông tại  có  Tính  theo

Giải

Ta có:

02 TỈ SỐ LƯỢNG GIÁC CỦA HAI GÓC PHỤ NHAU

…………………