Hướng dẫn giải nhanh toán 8 CTST bài 3: Hàm số bậc nhất y = ax + b (a≠0)
Baivan.net sẽ đưa ra lời giải nhanh, ngắn gọn chuẩn xác môn toán 8 bộ sách chân trời sáng tạo bài 3: Hàm số bậc nhất y = ax + b (a≠0). Học sinh kéo xuống để tham khảo. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt hiệu quả cao trong học tập
Bài tập 1 trang 22 sgk Toán 8 tập 2 CTST: Tìm các hàm số bậc nhất trong các hàm số sau đây và xác định các hệ số a, b của chúng
a) y = 4x + 2
b) y = 5 - 3x
c) $y =2+x^{2}$
d) y = -0.2x
e) $y=\sqrt{5}x-1$
Hướng dẫn giải:
a) y = 4x + 2 là hàm số bậc nhất với a = 4, b = 2
b) y = 5 - 3x là hàm số bậc nhất với a = -3 , b = 5
c) $y =2+x^{2}$ không là hàm số bậc nhất
d) y = -0.2x là hàm số bậc nhất với a = -0.2, b = 0
e) $y=\sqrt{5}x-1$ là hàm số bậc nhất với $a=\sqrt{5},b=-1$
Bài tập 2 trang 22 sgk Toán 8 tập 2 CTST: Với giá trị nào của m thì mỗi hàm số sau đây là hàm số bậc nhất?
a) y = (m - 1)x + m
b) y = 3 - 2mx
Hướng dẫn giải:
a) Điều kiện để hàm số y = (m - 1)x + m là hàm số bậc nhất là $m-1\neq 0$ suy ra $m\neq 1$
b) Điều kiện để hàm số y = 3 - 2mx là hàm số bậc nhất là $-2m\neq 0$ suy ra $m\neq 0$
Bài tập 3 trang 22 sgk Toán 8 tập 2 CTST:
a) Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:
y = x; y = x +2; y = -x; y = -x + 2
b) Bốn đồ thị nói trên cắt nhau tại các điểm O(0;0), A, B, C. Tứ giác có 4 đỉnh O, A, B, C là hình gì? Giải thích.
Hướng dẫn giải:
a) Với hàm số y = x, cho x = 1 thì y = 1. Đồ thị hàm số y = x đi qua các điểm O(0;0) và C(1;1)
Với hàm số y = x+2, cho x = 0 thì y = 2, cho x = -1 thì y = 1. Đồ thị hàm số y = x +2 đi qua các điểm B(0;2) và A(-1;1)
Với hàm số y = -x, cho x = -1 thì y = 1. Đồ thị hàm số y = -x đi qua các điểm O(0;0) và A(-1;1)
Với hàm số y = -x +2, cho x =0 thì y = 2, cho x = 1 thì y = 1. Đồ thị hàm số y = -x +2 đi qua các điểm B (0;2) và C(1;1)
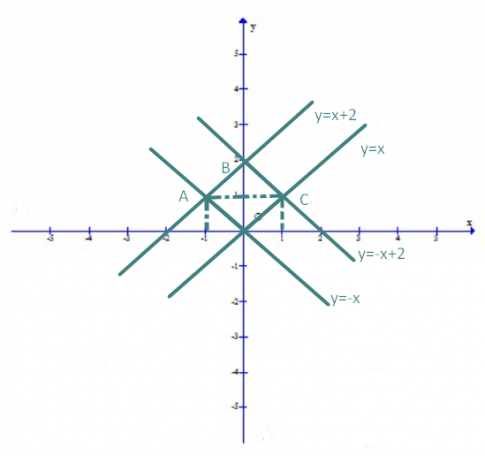
b) Ta có: Đường thắng y = x song song với đường thẳng y = x +2 suy ra OC // AB
Đường thẳng y = -x song song với đường thẳng y = -x +2 suy ra OA // BC
Tứ giác OABC có: OC // AB, OA // BC và $OB \perp AC$ suy ra OABC là hình thoi
Bài tập 4 trang 22 sgk Toán 8 tập 2 CTST: Để đổi nhiệt độ từ F (Fehrenheit) sang độ (Celsius), ta dùng công thức $C=\frac{5}{9}(F-32)$
a) C có phải hàm số bậc nhất theo biến số F không?
b) Hãy tính C khi F = 32 và tính F khi C = 100

Hướng dẫn giải:
a) Ta có: $C=\frac{5}{9}(F-32)\Leftrightarrow C=\frac{5}{9}F-\frac{160}{9}$ (*)
Hàm số $C=\frac{5}{9}F-\frac{160}{9}$ (theo biến số F) có dạng y = ax + b với $a=\frac{5}{9}\neq 0,b=-\frac{160}{9}$ nên $C=\frac{5}{9}F-\frac{160}{9}$ là hàm số bậc nhất theo biến số F.
b) Khi F = 32, thế vào (*)$\Rightarrow C=\frac{5}{9}\times 32-\frac{160}{9}=0(^{\circ}C)$
Khi C = 100, thế vào (*) $\Rightarrow 100=\frac{5}{9}F-\frac{160}{9}\Leftrightarrow F=212 $
Bài tập 5 trang 22 sgk Toán 8 tập 2 CTST: Gọi C và r lần lượt là chu vi và bán kính của một đường tròn. Hãy chứng tỏ C là một hàm số bậc nhất theo biến số r. Tìm hệ số a, b của hàm số này.
Hướng dẫn giải:
Công thức tính chu vi hình tròn là: $C = 2\pi r$
Hàm số $C=2\pi r$ có dạng y = ax + b với $a=2\pi \neq 0$ và b = 0 nên C là một hàm số bậc nhất theo biến số r
Bài tập 6 trang 22 sgk Toán 8 tập 2 CTST: Một người đi bộ trên đường thẳng với tốc độ v (km/h). Gọi s (km) là quãng đường đi được trong t (giờ)
a) Lập công thức tính s theo t
b) vẽ đồ thị của hàm số s theo biến số t khi v = 4
Hướng dẫn giải:
a)s = vt
b) Hàm số: s = 4t
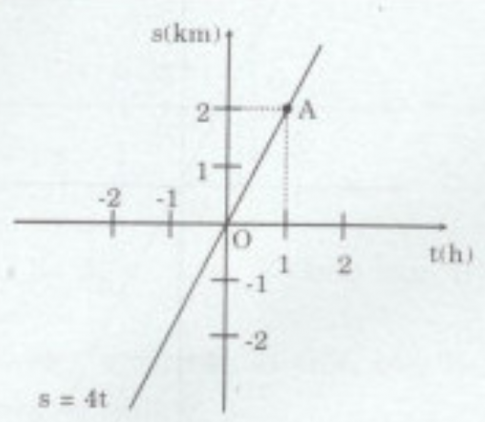
Đồ thị hàm số s = 4t là đường thẳng đi qua 2 điểm O(0; 0); $A(\frac{1}{2};2)$
