Giải chi tiết Toán 8 kết nối mới bài 12: Hình bình hành

1. Hình bình hành và tính chất

Hoạt động 1 trang 57 sgk Toán 8 tập 1 KNTT: Trong hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?

Hướng dẫn trả lời:

Hình c) là hình bình hành, bởi có các cặp cạnh song song

Hoạt động 2 trang 58 sgk Toán 8 tập 1 KNTT: Hãy nêu các tính chất của hình bình hành mà em biết

Hướng dẫn trả lời:

Các cạnh đối song song và bằng nhau.

Các góc đối bằng nhau.

Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

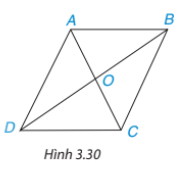
Hoạt động 3 trang 58 sgk Toán 8 tập 1 KNTT: Cho hình bình hành ABCD (H.3.30)

a) Chứng minh $\Delta ABC=\Delta CDA$. Từ đó suy ra AB = CD, AD = BC và $\widehat{ABC}=\widehat{CDA}$

b) Chứng minh $\Delta ABD=\Delta CDB$. Từ đó suy ra $\widehat{DAB}=\widehat{BCD}$

c) Gọi giao điểm của hai đường chéo AC, BD là O. Chứng minh $\Delta AOB=\Delta COD$. Từ đó suy ra OA = OC, OB = OD

Hướng dẫn trả lời:

a) Xét tam giác ABC và CDA ta có:

$\widehat{BAC}=\widehat{DCA}$ (hai góc so le trong, AB // CD)

AC chung

$\widehat{ACB}=\widehat{CAB}$ (hai góc so le trong, AD // BC)

Suy ra, $\Delta ABC=\Delta CDA$ (g.c.g)

Từ đó suy ra AB = CD, AD = BC và $\widehat{ABC}=\widehat{CDA}$

b) Xét tam giác ABD và CDB ta có:

$\widehat{ABD}=\widehat{CDB}$ (hai góc so le trong, AB // DC)

BD chung

$\widehat{ADB}=\widehat{CBD}$ (hai góc so le trong, AD // BC)

Suy ra $\Delta ABD=\Delta CDB$ (g.c.g)

Từ đó suy ra $\widehat{DAB}=\widehat{BCD}$

c) Xét tam giác AOB và COD ta có:

$\widehat{OAB}=\widehat{OCD}$ (hai góc so le trong, AB // DC)

AB = CD (cmt)

$\widehat{OBA}=\widehat{ODC}$ (hai góc so le trong, AB // DC)

Suy ra $\Delta AOB=\Delta COD$ (g.c.g)

Từ đó suy ra OA = OC, OB = OD

Luyện tập 1 trang 58 sgk Toán 8 tập 1 KNTT: Cho tam giác ABC. Từ một điểm M tùy ý trên cạnh BC, kẻ đường thẳng song song với AB, cắt cạnh AC tại N và kẻ đường thẳng song song với AC, cắt cạnh AB tại P. Gọi I là trung điểm của đoạn NP. Chứng minh rằng I cũng là trung điểm của đoạn AM.

Hướng dẫn trả lời:

Xét tứ giác ANMP ta có: AN // MP, AP // PM suy ra ANMP là hình bình hành

AM và PN là hai đường chéo của hình bình hành ANMP, I là trung điểm của PN, suy ra I cũng là trung điểm của AM

2. Dấu hiệu nhận biết

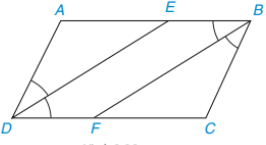
Luyện tập 2 trang 60 sgk Toán 8 tập 1 KNTT: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E và tia phân giác của góc B cắt CD tại F (H.3.32)

a) Chứng minh hai tam giác ADE và CBF là những tam giác cân, bằng nhau

b) Tứ giác DEBF là hình gì? Tại sao?

Hướng dẫn trả lời:

a) Ta có: $\widehat{ADE}=\widehat{EDC}$ (DE là phân giác góc D)

$\widehat{AED}=\widehat{EDC}$ (so le trong)

Suy ra $\widehat{AED}=\widehat{ADE}\Rightarrow $ tam giác ADE là tam giác cân

Tương tự, ta chứng minh được tam giác CBF là tam giác cân

b) Xét tam giác ADE và CBF ta có:

AD = CB

$\widehat{A}=\widehat{B}$

AE = CF

Suy ra $\Delta ADE=\Delta CBF$ (c.g.c) $\Rightarrow DE =BF$ (1)

Ta có: $\widehat{EDF}=\widehat{CBF},\widehat{CBF}=\widehat{CFB}$

$\Rightarrow \widehat{EDF}=\widehat{CFB}$. Mà hai góc này ở vị trí đồng vị suy ra DE // BF (2)

Từ (1) và (2) suy ra BEBF là hình bình hành

Luyện tập 3 trang 61 sgk Toán 8 tập 1 KNTT: Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi A', B' là các điểm sao cho O là trung điểm của AA', BB'. Chứng minh rằng A'B' = AB và đường thẳng A'B' song song với đường thẳng AB.

Hướng dẫn trả lời:

Xét tứ giác ABA'B' ta có: AA' và BB' là hai đường chéo của tứ giác; O là trung điểm của mỗi đường, suy ra ABA'B' là hình bình hành

Từ đó suy ra A'B' = AB và A'B' // AB.

Vận dụng trang 61 sgk toán 8 tập 1 KNTT:

Trở lại bài mở đầu. Em hãy vẽ hình và nêu cách vẽ con đường cần mở.

Hướng dẫn trả lời:

- Gọi C là giao điểm của a và b. 

- Lấy điểm D sao cho O là trung điểm của đoạn DC. 

- Từ D vẽ đường thẳng song song với a, cắt b tại B.

- Từ D vẽ đường thẳng song song với b, cắt a tại A 

- Ta có AB và CD là hai đường chéo của hình bình hành ADBC

 AB cắt CD tại O nên OA = OB.

Hình minh họa:

Bài tập

Bài tập 3.13 trang 61 sgk Toán 8 tập 1 KNTT: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?

a) Hình thang có hai cạnh bên song song là hình bình hành

b) Hình thang có hai cạnh bên bằng nhau là hình bình hành

c) Tứ giác có hai cạnh đối nào cũng song song là hình bình hành

Hướng dẫn trả lời:

a) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

b) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

c) Đúng,  vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

Bài tập 3.14 trang 61 sgk Toán 8 tập 1 KNTT: Tính các góc còn lại của hình bình hành ABCD trong Hình 3.35.

Hướng dẫn trả lời:

$\widehat{C}=\widehat{A}=100^{\circ}$

$\widehat{D}=\widehat{B}=180^{\circ}-\widehat{A}=180^{\circ}-100^{\circ}=80^{\circ}$

Bài tập 3.15 trang 61 sgk Toán 8 tập 1 KNTT: Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh BF = DE.

Hướng dẫn trả lời:

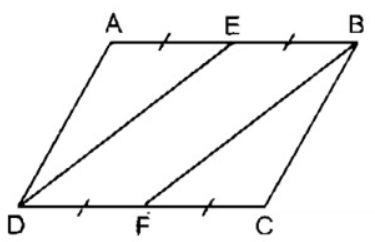
Ta có: AB = CD (tính chất hình bình hành)

EB = $\frac{1}{2}$ AB (gt)

FD = $\frac{1}{2}$ CD (gt)

Suy ra: EB = FD (1)

Mà AB // CD (gt)

⇒ BE // FD (2)

Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ DE = BF (tính chất hình bình hành)

Bài tập 3.16 trang 61 sgk Toán 8 tập 1 KNTT: Trong mỗi trường hợp sau đây, tứ giác nào là hình bình hành, tứ giác nào không là hình bình hành? Vì sao?

Hướng dẫn trả lời:

a) $\widehat{D}=80^{\circ}$, ABCD là hình bình hành vì có các góc đối bằng nhau.

b) $\widehat{B}=120^{\circ}$, ABCD không là hình bình hành vì có cặp góc đối không bằng nhau.

c) $\widehat{C}=70^{\circ}$, ABCD là hình bình hành vì có các góc đối bằng nhau.

Bài tập 3.17 trang 61 sgk Toán 8 tập 1 KNTT: Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:

a) Hai tứ giác AEFD, AECF là những hình bình hành

b) EF = AD, AF = EC

Hướng dẫn trả lời:

a) ABCD là hình bình hành => AE // CF; AE // DF

Mà E và F là trung điểm của AB và CD.

=> AE = EB = DF = FC 

+ Xét tứ giác AECF có: AE // CF và AE = FC => AECF là hình bình hành.

+ Xét tứ giác AEFD có: AE // DF và AE = DF => AEFD là hình bình hành.

b)  + AFCE là hình bình hành (chứng minh trên) => AF = EC 

     + ADFE là hình bình hành (chứng minh trên ) => EF = AD

Bài tập 3.18 trang 61 sgk Toán 8 tập 1 KNTT: Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh $\Delta OAM=\Delta OCN$. Từ đó suy ra tứ giác MBND là hình bình hành

Hướng dẫn trả lời:

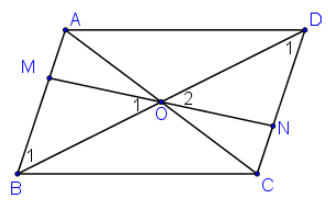
Xét tam giác OAM và OCN ta có:

$\widehat{AOM}=\widehat{CON}$ (đối đỉnh)

OA = ON

$\widehat{OAM}=\widehat{OCN}$ (so le trong)

Suy ra, $\Delta OAM=\Delta OCN$ (g.c.g) do đó AM = CN

Lại có AB = CD, suy ra MB = ND 

Ta có : MB = ND, MB// ND $\Rightarrow $ tứ giác MBND là hình bình hành