Hướng dẫn giải nhanh Toán 8 KNTT Bài tập cuối chương II
Baivan.net sẽ đưa ra lời giải nhanh, ngắn gọn chuẩn xác môn toán 8 bộ sách kết nối tri thức và cuộc sống Bài tập cuối chương II. Học sinh kéo xuống để tham khảo. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt hiệu quả cao trong học tập
TRẮC NGHIỆM
Bài 2.28 – 2.31. Trang 47 sgk toán 8 tập 1
Đáp án:
2.28. B | 2.29. D | 2.30. D | 2.31. C |
Giải chi tiết:
Câu 2.28:
$x^2 - 9x + 8 = x^2 - 8x – x + 8 = (x^2 - 8x) - (x – 8)$
= $x(x – 8) – (x – 8) = (x - 1)(x - 8)$
Câu 2.29:
$A^2 – B^2 = (A-B)(A+B)$.
Câu 2.30:
$25x^2 + 20xy + 4y^2 = (5x)^2 + 2.5x.2y + (2y)^2 = (5x + 2y)^2$
Câu 2.31:
$A = (2x + 1)^3 - 6x(2x + 1)$
= $8x^3 +12x^2 + 6x + 1 - 12x^2 - 6x = 8x^3 + 1$
TỰ LUẬN
Bài 2.32. Trang 47 sgk toán 8 tập 1
Tính nhanh giá trị của các biểu thức:
Đáp án:
a) $x^2 - 4x + 4 = (x – 2)^2$
Tại $x = 102$ ta có : $(102-2)^2 = 100^2 = 10 000$.
b) $x^3 + 3x^2 + 3x + 1 = (x +1)^3$
Tại $x = 999$ ta có : $(999 + 1)^3 = 1 000^3 = 1 000 000 000$
Bài 2.33. Trang 47 sgk toán 8 tập 1
Rút gọn các biểu thức:
a) $(2x - 5y)(2x + 5y) + (2x + 5y)^2$
b) $(x + 2y)(x^2 - 2xy + 4y^2) + (2x - y)(4x^2 + 2xy + y^2)$
Đáp án:
a) $(2x - 5y)(2x + 5y) + (2x + 5y)^2$
= $4x^2 - 25y^2 + 4x^2 + 20xy + 25y^2 = 8x^2 + 20xy$
b) $(x + 2y)(x^2 - 2xy + 4y^2) + (2x - y)(4x^2 + 2xy + y^2)$
= $x^3 + (2y)^3 + (2x)^3 – y^3 = x^3 + 8y^3 + 8x^3 – y^3 = 9x^3 + 7y^3$
Bài 2.34. Trang 47 sgk toán 8 tập 1
Phân tích đa thức sau thành nhân tử:
$6x^2 - 24y^2$
$64x^3 - 27y^3$
$x^4 - 2x^3 + x^2$
$(x – y)^3 + 8y^3$
Đáp án:
a) $6x^2 - 24y^2 = 6.(x^2 - 4y^2) = 6(x-2y)(x+2y)$
b) $(4x)^3 – (3y)^3 = (4x - 3y)[(4x)^2 + 4x.3y + (3y)^2]$
= $(4x - 3y)(16x^2 + 12xy + 9y^2)$
c) $x^4 - 2x^3 + x^2 = x^2.(x^2 - 2x + 1) = x^2.(x – 1)^2$
d) $(x – y)^3 + (2y)^3 = (x – y + 2y)[(x – y)^2 – (x – y).2y + (2y)^2]$
= $(x + y)(x^2 - 2xy + y^2 - 2xy + 2y^2 + 4y^2)$
= $(x + y)(x^2 + 7y^2 - 4xy)$
Bài 2.35. Trang 47 sgk toán 8 tập 1
Sử dụng hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách…
Đáp án:
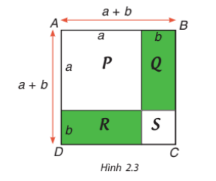
Cách 1 :
$S_{ABCD} = (a + b)^2$
Cách 2 :
$S_{ABCD} = S_{P} + S_{R} + S_{Q} + S_{S}$
= $a^2 + ab + ab + b^2 = a^2 + 2ab + b^2$
Do đó $(a + b)^2 = a^2 + 2ab + b^2$.
