Hướng dẫn giải nhanh Toán 8 KNTT bài 16: Đường trung bình của tam giác

TÍNH CHẤT ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC

HĐ1. Trang 82 sgk toán 8 tập 1

Cho DE là đường trung bình của tam giác ABC (H.4.15).Sử dụng định lí Thales đảo, chứng minh rằng DE // BC.

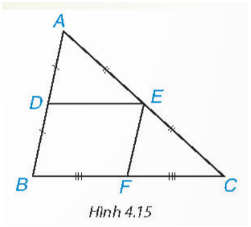
Đáp án:

$AE = EC$ và $E\in AC \Rightarrow E$ là trung điểm của AC

$AD = BD$ và $D\in AB \Rightarrow D$ là trung điểm của AB

ΔABC có E, D lần lượt là trung điểm của AC và AB, theo định lí Thalès đảo 

$\Rightarrow DE // BC (đpcm)$.

HĐ2. Trang 82 sgk toán 8 tập 1

Cho DE là đường trung bình của tam giác ABC (H.4.15). Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành…

Đáp án:

$EC = \frac{1}{2}AC; CF = \frac{1}{2}BC \Rightarrow EF // AB$ (theo định lí Thalès đảo).

$AD = \frac{1}{2}AB; AE = \frac{1}{2}AC \Rightarrow DE // BC$ (theo định lí Thalès đảo).

Xét tứ giác BDEF có $EF // BD; DE // BF \Rightarrow BDEF$ là hình bình hành

$\Rightarrow DE = BF$ mà $BF = \frac{1}{2}BC \Rightarrow DE = \frac{1}{2}BC$.

Luyện tập. Trang 83 sgk toán 8 tập 1

Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?

Đáp án:

Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác $ABC \Rightarrow DE // BC \Rightarrow BDEC$ là hình thang

ΔABC cân tại tại $A \Rightarrow  \widehat{B} = \widehat{C} \Rightarrow BDEC$ là hình thang cân.

GIẢI BÀI TẬP CUỐI SGK

Bài 4.6. Trang 83 sgk toán 8 tập 1

Tính các độ dài x, y trong Hình 4.18.

Đáp án:

a). ΔEDF có H, K lần lượt là trung điểm của $DF, EF \Rightarrow HK$ là

đường trung bình của $ΔEDF \Rightarrow HK = \frac{1}{2}DE = \frac{1}{2}x = 3$

$\Rightarrow x= 6$

b) MN // AC. ( cùng $\perp AB$)

$AM = BM = 3 \Rightarrow M$ là trung điểm của AB

$\Rightarrow MN$ là đường trung bình của Δ ABC.

$\Rightarrow y = CN = NB = 5$.

Bài 4.7. Trang 83 sgk toán 8 tập 1

Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.

a) Chứng minh tứ giác BMNC là hình thang

b) Tứ giác MNPB là hình gì? Tại sao?

Đáp án:

a) MN là đường trung bình của $ΔABC \Rightarrow MN // BC$ 

Tứ giác MNCB có NM // BP nên MNCB là hình thang (đpcm).

b) NP là đường trung bình của $ΔABC \Rightarrow NP // AB$

Tứ giác MBNP có MB // NP; MN // BP (cmt).

$\Rightarrow$ Tứ giác MBNP là hình bình hành.

Bài 4.8. Trang 83 sgk toán 8 tập 1

Cho tam giác ABC có trung tuyến AM. Lấy hai điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E…

Đáp án:

a) Xét Δ BCD có M,E lần lượt là trung điểm của $BC, BD \Rightarrow EM$ là đường trung bình $\Rightarrow EM // DC (đpcm)$

b) $AD = DE \Rightarrow D$ là trung điểm của AE 

DI // EM 

$\Rightarrow DI$ là đường trung bình của $ΔAME \Rightarrow I$ là trung điểm của AM.(đpcm)

Bài 4.9. Trang 83 sgk toán 8 tập 1

Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh rằng tứ giác AHOK là hình chữ nhật.

Đáp án:

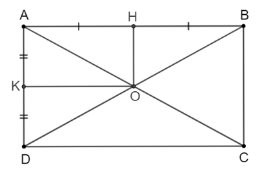
Vì ABCD là hình chữ nhật nên O là trung điểm của hai đường chéo AC và BD.

Xét ΔABD có OH là đường trung bình $\Rightarrow OH // AD$

Chứng minh tương tự ta được: $OK // AB$ 

Tứ giác AKOH có $OK // AH , OH // AK \Rightarrow AKOH$ là hình bình hành. Mà  $\widehat{A} = 90^{\circ} \Rightarrow AKOH$ là hình chữ nhật (đpcm).