Hướng dẫn giải nhanh Toán 8 KNTT bài 10: Tứ giác
Baivan.net sẽ đưa ra lời giải nhanh, ngắn gọn chuẩn xác môn toán 8 bộ sách kết nối tri thức và cuộc sống bài 10: Tứ giác. Học sinh kéo xuống để tham khảo. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt hiệu quả cao trong học tập
I. TỨ GIÁC LỒI
Luyện tập 1. Trang 49 sgk toán 8 tập 1
Quan sát tứ giác ABCD trong hình 3.4…
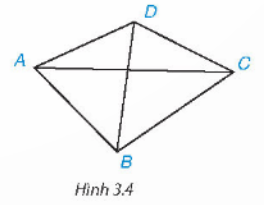
Đáp án:
Đường chéo còn lại là BD.
Cặp cạnh AD, BC là cặp cạnh đối.
Cặp góc B, D là cặp góc đối.
II. TỔNG CÁC GÓC CỦA MỘT TỨ GIÁC
HĐ. Trang 50 sgk toán 8 tập 1
Cho tứ giác ABCD. Kẻ đường chéo BD (H3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối …
Đáp án:
Áp dụng định lí tổng ba góc trong một tam giác ta có:
∆CBD có: $\widehat{C} + \widehat{B_2} + \widehat{D_2} = 180^{\circ}$
∆ABD có: $\widehat{A}+\widehat{B_1}+\widehat{D_1} =180^{\circ}$
$\Rightarrow \widehat{C} + \widehat{B_2} + \widehat{D_2} + \widehat{A} + \widehat{B_1} + \widehat{D_1}$ = $180^{\circ} + 180^{\circ}$
$\Rightarrow \widehat{A} + \widehat{B} +\widehat{C} + \widehat{D} = 360^{\circ}$
Luyện tập 2. Trang 50 sgk toán 8 tập 1
Cho tứ giác EFGH như hình 3.7, hãy tính góc F
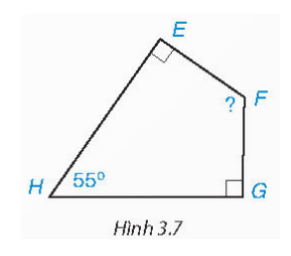
Đáp án:
Theo định lí ta có:
$\widehat{E} + \widehat{F} + \widehat{G} + \widehat{H} =360^{\circ}$
$\Rightarrow \widehat{F} + 90^{\circ} + 90^{\circ} + 55^{\circ} = 360^{\circ}$
$\Rightarrow \widehat{F} = 360^{\circ} - 90^{\circ} + 90^{\circ} + 55^{\circ} =125^{\circ}$
Vận dụng. Trang 50 sgk toán 8 tập 1
Giải bài toán ở mở đầu
Đáp án:
Ta có thể ghép được bốn tứ giác khít nhau.
Khi đó, có 1 điểm chung tại 4 đỉnh của 4 tứ giác.
Tổng số đo góc của 4 góc đó bằng 360º
III. GIẢI BÀI TẬP CUỐI SGK
Bài 3.1. Trang 51 sgk toán 8 tập 1
Tính góc chưa biết của các tứ giác trong hình 3.8

Đáp án:
a) $\widehat{C} = 360^{\circ} - \widehat{A} - \widehat{B} - \widehat{D} = 360^{\circ} - 90^{\circ} . 3 = 90^{\circ}$
b) $\widehat{S}=180^{\circ} - 110^{\circ} = 70^{\circ}$
$\widehat{U}=180^{\circ} - 60^{\circ} = 120^{\circ}$
$\widehat{R} = 360^{\circ} - \widehat{V} - \widehat{S} - \widehat{U} = 360^{\circ} - 90^{\circ} - 70^{\circ} - 120^{\circ} = 80^{\circ}$
Bài 3.2. Trang 51 sgk toán 8 tập 1
Tính góc chưa biết của tứ giác trong hình 3.9 biết rằng….

Đáp án:
Ta có :
$\widehat{E} + \widehat{F} + \widehat{G} + \widehat{H} =360^{\circ} (1)$
Mà $\widehat{H} = \widehat{E} +10^{\circ}$, thay vào (1) ta có :
$\widehat{H} - 10^{\circ} + \widehat{F} + \widehat{G} + \widehat{H} =360^{\circ}$
$\Rightarrow 2\widehat{H} =360^{\circ} - 60^{\circ} + 10^{\circ} = 260^{\circ}$
$\Rightarrow \widehat{H} =130^{\circ}; \widehat{E} = 120^{\circ}$
Bài 3.3. Trang 51 sgk toán 8 tập 1
Tứ giác ABCD trong hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”…

Đáp án:
a) Xét ∆CBD có CB = CD (gt), suy ra ∆CBD cân tại C
=> đường trung trực của BD đi qua điểm C (1).
Xét ∆ABD có AD = AB (gt), suy ra ∆ABD cân tại A
=> đường trung trực của BD đi qua điểm A (2).
Từ (1) và (2) suy ra AC là trung trực của BD.
b) Xét ∆ABC và ∆ADC có:
$AC chung; AB = AD (gt); BC = CD (gt)$
=> ∆ABC = ∆ADC (c.c.c)
$\Rightarrow \widehat{ABC} = \widehat{ADC}$
Ta có:
$\widehat{DAB} + \widehat{BCD} + \widehat{ABC} + \widehat{CDA}=360^{\circ}$
$\Rightarrow 100^{\circ} + 60^{\circ} + 2\widehat{B} = 360^{\circ}$
=> $\widehat{B} = ( 360^{\circ} – 100^{\circ} – 60^{\circ} ) : 2 = 100^{\circ}$
=> $\widehat{B} = \widehat{D} = 100^{\circ}$
