Hướng dẫn giải nhanh Toán 8 KNTT bài 13: Hình chữ nhật

HÌNH CHỮ NHẬT

HĐ1. Trang 64 sgk toán 8 tập 1

Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?

Đáp án:

Hình b là hình chữ nhật vì có 4 góc vuông.

HĐ2. Trang 64 sgk toán 8 tập 1

Hình chữ nhật có là hình bình hành không, có là hình thang cân không? Tại sao?

Đáp án:

Hình chữ nhật là hình bình hành vì có các cặp cạnh đối song song và bằng nhau

Hình chữ nhật là hình thang cân vì có cặp góc ở đáy bằng nhau.

Luyện tập 1. Trang 65 sgk toán 8 tập 1

Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O…

Đáp án:

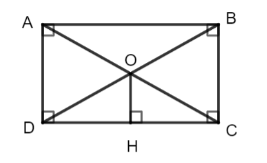
Xét Δ OHC và Δ OHD : 

Chung cạnh OH

OC = OD

$\Rightarrow Δ OHC = Δ OHD (ch – cgv)$

$\Rightarrow HC = HD \Rightarrow H$ là trung điểm của DC.

DẤU HIỆU NHẬN BIẾT

HĐ3. Trang 65 sgk toán 8 tập 1

Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có là hình chữ nhật không? Vì sao?

Đáp án:

$\widehat{A} = \widehat{C} = 90^{\circ}$ ( hai góc đối nhau)

$\widehat{D} = 180^{\circ} - \widehat{A} = 90^{\circ}$ ( hai góc bù nhau)

$\widehat{D} = \widehat{B} = 90^{\circ}$ ( hai góc đối nhau)

$\widehat{A}= \widehat{B}= \widehat{C} = \widehat{D}  = 90^{\circ} \Rightarrow ABCD$ là hình chữ nhật

Luyện tập 2. Trang 66 sgk toán 8 tập 1

Cho tứ giác ABCD có $\widehat{A} = 90^{\circ}$, hai đường chéo cắt nhau tại trung điểm O của mỗi đường. Hỏi tứ giác ABCD là hình gì? Tại sao?

Đáp án:

Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường 

$\Rightarrow ABCD$ là hình bình hành.

Hình bình hành ABCD có: $\widehat{A} = 90^{\circ} \Rightarrow ABCD$ là hình chữ nhật.

GIẢI BÀI TẬP CUỐI SGK

Bài 3.25. Trang 66 sgk toán 8 tập 1

Bằng êke, nêu cách kiểm tra một tứ giác có là hình chữ nhật không. Hãy giải thích kết quả

Đáp án:

Khi dùng êke kiểm tra được ba góc của tứ giác là góc vuông thì tứ giác là hình chữ nhật.

Khi dùng êke kiểm tra có ít nhất một góc không vuông thì tứ giác đó không là hình chữ nhật.

Bài 3.26. Trang 66 sgk toán 8 tập 1

Bằng compa, nêu cách kiểm tra một tứ giác có là hình chữ nhật không. Hãy giải thích kết quả.

Đáp án: Kiểm tra các cặp cạnh đối:

Nếu không bằng nhau $\Rightarrow$ không là hình chữ nhật 

Nếu bằng nhau $\Rightarrow$ là hình bình hành

Kiểm tra hai đường chéo: 

Nếu không bằng nhau $\Rightarrow$ không là hình chữ nhật

Nếu bằng nhau $\Rightarrow$ là hình chữ nhật.

Bài 3.27. Trang 66 sgk toán 8 tập 1

Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.

Đáp án:

Hình tứ giác AHCN có hai đường chéo AC và HN cắt nhau tại M là trung điểm

của mỗi đường.

$\Rightarrow  AHCN$ là hình bình hành

Hình bình hành AHCN có $\widehat{AHC} = 90^{\circ} \Rightarrow AHCN$ là hình chữ nhật.

Bài 3.28. Trang 66 sgk toán 8 tập 1

Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC…

Đáp án:

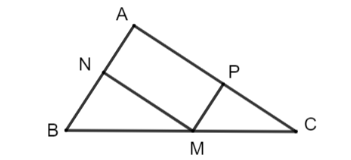
a) Tứ giác MPAN có  M=P=A=N =900 \Rightarrow MPAN$ là hình chữ nhật.

b) MPAN là hình chữ nhật $\Rightarrow AM = NP$

AM ngắn nhất khi $\widehat{AMC} = 90^{\circ}$

$\Rightarrow AM$ là đường cao của tam giác ABC

ΔABC cân tại A nên AM cũng là đường trung tuyến$\Rightarrow M$ là trung điểm BC.