Hướng dẫn giải nhanh Toán 8 KNTT bài Luyện tập chung trang 62

Bài 3.19. Trang 63 sgk toán 8 tập 1

Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?

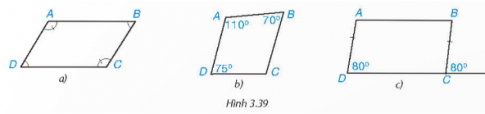
Đáp án:

a) ABCD là hình bình hành vì $\widehat{A} = \widehat{C}; \widehat{B} = \widehat{D}$

b) ABCD không phải là hình bình hành vì $\widehat{B} ≠ \widehat{D}$

c) ABCD là hình bình hành vì AD // BC và AD = BC 

Bài 3.20. Trang 63 sgk toán 8 tập 1

Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:…

Đáp án:

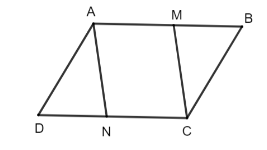
a) Tứ giác AMCN có  AM // CN và AM = CN (gt)

$\Rightarrow AMCN$ là hình bình hành $\Rightarrow AN = MC$

b) AMCN là hình bình hành( chứng minh trên)

$\Rightarrow \widehat{AMC} = \widehat{ANC}$

Bài 3.21. Trang 63 sgk toán 8 tập 1

Vẽ tứ giác ABCD theo hướng dẫn sau:…

Đáp án:

Do AB //CD và A, D nằm cùng phía đối với đường thẳng BC 

$\Rightarrow ABCD$ là một tứ giác.

Vì AB // CD  và AB = CD nên tứ giác ABCD là hình bình hành.

Bài 3.22. Trang 63 sgk toán 8 tập 1

Cho hình bình hành ABC có AB = 3 cm, AD = 5 cm. 

a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?

b) Tính khoảng cách từ giao điểm đó đến điểm C

Đáp án:

a) Vì AD = BC = 5cm nên có duy nhất điểm E  cạnh BC thỏa mãn BE = 3cm

 ∆ABE cân tại $B ( AB = BE) \Rightarrow \widehat{BEA} = \widehat{BAE}$ 

Mà $\widehat{EAD} = \widehat{BEA}$ (so le trong)

$\Rightarrow \widehat{BAE} = \widehat{EAD}$

$\Rightarrow AE$ là tia phân giác của DAB .Tia này không cắt cạnh CD.

b) $EC = BC – EB = 5 – 3 = 2 cm.$

Bài 3.23. Trang 63 sgk toán 8 tập 1

Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:…

Đáp án:

a) $AB =AE : 2; CF =DF : 2; AB = DC \Rightarrow AB = CF$

$AE // DF \Rightarrow AB // CF \Rightarrow ABFC$ là hình bình hành

ABCD là hình bình hành $\Rightarrow AB // DC, AB = DC$

$\Rightarrow AE // DF, AE = DF \Rightarrow AEFD$ là hình bình hành

b) Hình bình hành ABFC có 2 đường chéo BC và AF cắt nhau tại O; O là trung điểm của AF và BC.

Hình bình hành AEFD có 2 đường chéo DE và AF cắt nhau tại O; O là trung điểm của AF và DE.

Vậy các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

Bài 3.24. Trang 63 sgk toán 8 tập 1

Cho ba điểm không thẳng hàng.

a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành. Hãy vẽ hình và mô tả cách tìm

b) Hỏi tìm được bao nhiêu điểm như vậy

Đáp án:

a) Ba điểm không thẳng hàng là A,B,C. Ta cần tìm điểm D sao cho ABCD là hình bình hành.

AC và BD là đường chéo thì AC và BD cắt nhau tại trung điểm mỗi đường. Từ trung điểm AC kẻ đoạn thẳng đối xứng với điểm B qua trung điểm ta được điểm

D (điểm $D_{2}$ trên hình)

b) Tương tự ta tìm được điểm $D_{1}$ và $D_{3}$

Vậy tìm được 3 điểm D thỏa mãn yêu cầu đề bài.