Hướng dẫn giải nhanh Toán 8 KNTT bài Luyện tập chung trang 87
Baivan.net sẽ đưa ra lời giải nhanh, ngắn gọn chuẩn xác môn toán 8 bộ sách kết nối tri thức và cuộc sống bài Luyện tập chung trang 87. Học sinh kéo xuống để tham khảo. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt hiệu quả cao trong học tập
Bài 4.13. Trang 88 sgk toán 8 tập 1
Tìm độ dài x trong Hình 4.30
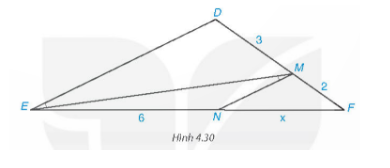
Đáp án:
$\widehat{NME} = \widehat{MED}$ ( so le trong) => ED // MN
$\frac{FN}{EN} = \frac{FM}{MD} \Rightarrow \frac{x}{6} = \frac{2}{3}$
=> x = 2 .6 : 3 = 4 (đvđd).
Bài 4.14. Trang 88 sgk toán 8 tập 1
Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC…
Đáp án:
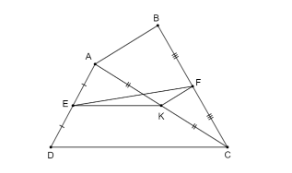
a) FK là đường trung bình Δ ABC => FK // AB.
KE là đường trung bình Δ ACD suy ra KE // CD.
b) FK là đường trung bình ΔABC
=> $FK = \frac{1}{2}AB$
KE là đường trung bình ΔACD
=> $KE = \frac{1}{2} CD$
$FK + KE = \frac{1}{2}(AB + CD)$ (1)
Bất đẳng thức tam giác Δ KEF, ta có:
$EF < FK + KE$ (2)
Từ (1) và (2) => $EF < \frac{1}{2}(AB + CD)$.
Bài 4.15. Trang 88 sgk toán 8 tập 1
Cho tam giác ABC, phân giác AD…
Đáp án:
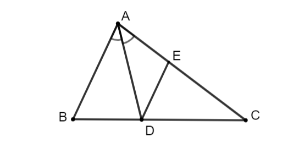
DE // AB, áp dụng định lí Thalès vào ΔABC, ta có : $\frac{EC}{EA} = \frac{DC}{DB}$ (1)
AD là tia phân giác của $\widehat{BAC}$
$\Rightarrow \frac{DC}{DB} = \frac{AC}{AB}$ (2)
Từ (1) và (2) => $\frac{AC}{AB} = \frac{EC}{EA}$ (đpcm).
Bài 4.16. Trang 88 sgk toán 8 tập 1
Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D…
Đáp án:
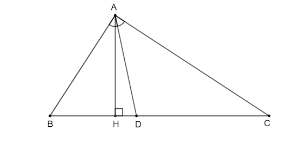
a) AD là đường phân giác
=> $\frac{BD}{CD} = \frac{AB}{AC}= \frac{15}{10} = \frac{3}{4}$
=> $\frac{BD}{3} = \frac{CD}{4}$
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
$\frac{BD}{3} = \frac{CD}{4} = \frac{BD+CD}{3+4} = \frac{BC}{7} = \frac{25}{7}$
$\Rightarrow BD = \frac{25}{7} . 3 = \frac{75}{7} (cm)$;
$\Rightarrow CD = \frac{25}{7} . 4 =\frac{100}{7} (cm)$.
b) Kẻ $AH\perp BC$
$S_{ACD}=\frac{1}{2} . CD . AH; S_{ABD} = \frac{1}{2} . BD . AH$
$\Rightarrow \frac{S_{ABD}}{S_{ACD}} = \frac{\frac{1}{2} . BD . AH}{\frac{1}{2} . CD . AH} = \frac{BD}{CD} = \frac{3}{4}$
Bài 4.17. Trang 88 sgk toán 8 tập 1
Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng:…
Đáp án:
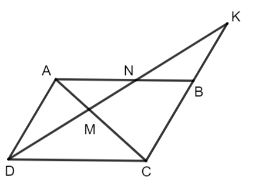
ΔADM có CK // AD, áp dụng định lí Thalès ta có : $\frac{MC}{AM} = \frac{MK}{MD}$ (1)
ΔAMN có AN // CD, áp dụng định lí Thalès ta có: $\frac{MC}{AM} = \frac{MD}{MN}$ (2)
Từ (1) và (2) => $\frac{MK}{MD} = \frac{MD}{MN} => MD^2 = MK.MN$ (đpcm)
