Tải giáo án Powerpoint chuyên đề Toán 11 chân trời sáng tạo mới nhất

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC MÔN TOÁN! 

KHỞI ĐỘNG 

Phép dời hình nào có thể biến hình ngôi sao A thành hình ngôi sao B? 

CHUYÊN ĐỀ 1: 

PHÉP BIẾN HÌNH PHẲNG 

BÀI 2. PHÉP TỊNH TIẾN 

NỘI DUNG BÀI HỌC 

ĐỊNH NGHĨA 

TÍNH CHẤT 

01 ĐỊNH NGHĨA 

HĐKP1 

Quan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1). 

1. a) Có nhận xét gì về các vectơ (AA′) ⃗, (BB′) ⃗,…,(EE^′) ⃗?
2. b) Có hay không phép biến hình biến các điểm A, B, C, D, E theo thứ tự thành các điểm A′, B′, C′, D′, E′?

Giải: 

1. a) Quan sát Hình 1, ta thấy các vectơ (AA^′) ⃗, (BB^′) ⃗, …(EE^′) ⃗ cùng hướng và có độ dài bằng nhau.

Vậy (AA^′) ⃗=(BB^′) ⃗=(CC^′) ⃗=(DD^′) ⃗=(EE) ⃗. 

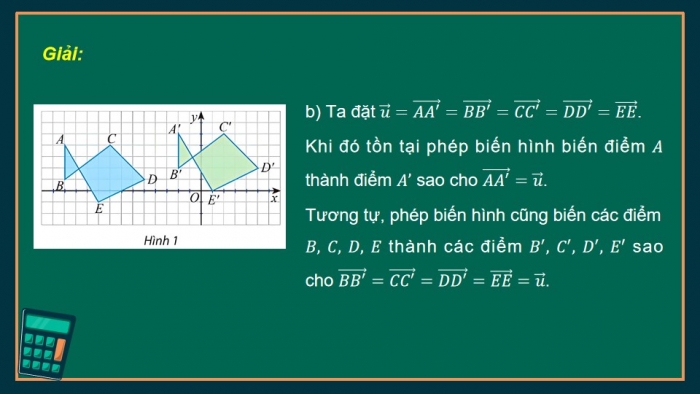
Giải: 

1. b) Ta đặt u ⃗=(AA^′) ⃗=(BB^′) ⃗=(CC^′) ⃗=(DD^′) ⃗=(EE) ⃗.

Khi đó tồn tại phép biến hình biến điểm A thành điểm A’ sao cho (AA^′) ⃗=u ⃗. 

Tương tự, phép biến hình cũng biến các điểm B, C, D, E thành các điểm B^′, C^′, D^′, E′ sao cho (BB^′) ⃗=(CC^′) ⃗=(DD^′) ⃗=(EE) ⃗=u ⃗. 

Định nghĩa 

Cho vectơ u ⃗, phép tịnh tiến theo vectơ u ⃗ là phép biến hình biến điểm M thành điểm M′ sao cho (MM^′) ⃗=u ⃗. 

Phép tịnh tiến theo vectơ u ⃗ được kí hiệu là T_u ⃗ và u ⃗ gọi là vectơ tịnh tiến. 

Chú ý: Nếu M′ là ảnh của điểm M qua phép tịnh tiến T_u ⃗ thì ta kí hiệu         M^′=T_u ⃗(M). 

Ví dụ 1. Cho phép tịnh tiến T_u ⃗ biến điểm M thành điểm M′. Tìm phép biến hình biến điểm M′ thành điểm M. 

Giải: 

Ta có: T_u ⃗(M)=M′ nên (MM^′) ⃗=u ⃗, suy ra (M^′M) ⃗=−u ⃗, do đó T_−u ⃗(M^′)=M. 

Vậy phép tịnh tiến theo vectơ −u ⃗ biến điểm M′ thành điểm M. 

Ví dụ 2. Trong mặt phẳng toạ độ Oxy, cho phép biến hình f biến điểm M(x; y) thành điểm M′(x′; y′) thoả mãn: 

{█(x^′=x+a@y^′=y+b)┤ với a,b là hai số không đổi cho trước. 

Chứng minh f là một phép tịnh tiến và tìm toạ độ của vectơ tịnh tiến. 

Giải: 

Ta có (MM^′) ⃗=(x^′−x;y^′−y)=(a;b). Đặt u ⃗=(a;b).  

Vậy f là một phép tịnh tiến theo vectơ u ⃗=(a;b). 

CHÚ Ý 

Người ta gọi {█(x^′=x+a@y^′=y+b)┤  là biểu thức tọa độ của phép tịnh tiến biến điểm M(x;y) thành điểm M^′(x^′;y^′) theo vectơ u ⃗=(a;b). 

Thực hành 1 

Chứng minh phép đồng nhất là một phép tịnh tiến. 

Giải: 

Giả sử A′ là ảnh của A qua phép đồng nhất f⇒A^′=f(A) 

⇒A′≡A hay AA^′=0 

Khi đó (AA^′) ⃗=0 ⃗ 

Tương tự như vậy, mỗi điểm M bất kì ta lấy điểm M′ là ảnh của M qua phép đồng nhất f⇒ (MM^′) ⃗=0 ⃗ 

Vậy phép đồng nhất là một phép tịnh tiến theo vectơ 0 ⃗. 

Vận dụng 1. Tìm độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ v ⃗ biến các điểm A, B, C, D, E thành A’, B’, C’, D’, E’ trong Hoạt động khám phá 1 (biết cạnh mỗi ô vuông là 1 đơn vị). 

Giải: 

Đặt v ⃗=(AA′) ⃗=(BB′) ⃗= (CC′) ⃗=(DD′) ⃗ =(EE′) ⃗ 

Dựng ∆AA’M vuông tại M (như hình vẽ). 

Khi đó, phép tịnh tiến theo v ⃗ biến các điểm A, B, C, D, E thành các điểm A^′, B^′, C^′, D^′, E^′. 

Dựng ∆AA′M vuông tại M. 

Ta thấy AM=1 (đvđd); AM=10 (đvđd) 

⇒ AA^′=√AM^2+A^′M^2=√1^2+10^2 

  =√101  

Khi đó |v ⃗|=|(AA^′) ⃗|=AA^′=√101. 

02 TÍNH CHẤT 

HĐKP2 

Cho vectơ u ⃗ và đường thẳng d. A và M là hai điểm bất kì trên d. Gọi A′ và M′ lần lượt là ảnh của A và M qua phép tịnh tiến T_u ⃗. 

1. a) Hai vectơ (A′M^′) ⃗, (AM) ⃗ có bằng nhau không?
2. b) Khi điểm M thay đổi trên d thì điểm M’ thay đổi như thế nào? Giải thích.

Giải: 

1. a) Ta có T_u ⃗(A)=A^′⇒(AA^′) ⃗=u ⃗;     T_u ⃗(M)=M′⇒(MM^′) ⃗=u ⃗

Khi đó (AA^′) ⃗=(MM^′) ⃗=u ⃗   

⇒ AA^′=MM′ và AA^′//MM′ 

Vậy tứ giác AMM′A là hình bình hành ⇒ (A^′M^′) ⃗=(AM) ⃗ 

1. b) Gọi d′ là giá của (A^′M^′) ⃗

    Vì A^′M^′//AM ⇒ d^′//d 

    Vậy khi M thay đổi trên d thì M′ thay đổi trên d′ thỏa mãn (MM^′) ⃗=u ⃗. 

Tính chất 

Phép tịnh tiến là một phép dời hình. 

Phép tịnh tiến có đầy đủ tính chất của phép dời hình. 

Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó. 

Các xác định ảnh của một đoạn thẳng, đường thẳng,     tam giác, đường tròn qua phép tịnh tiến. 

Đoạn thẳng MN: Xác định ảnh M^′, N′ của hai đầu mút M, N. Vẽ đoạn thẳng M′N′. 

Đường thẳng d đi qua M: Xác định ảnh M′ của M. Vẽ d′ đi qua M′ và song song hoặc trùng với d. 

Tam giác ABC: Xác định ảnh A^′, B^′, C′ của ba đỉnh A, B, C. Vẽ tam giác A^′B^′C′. 

Đường tròn tâm O, bán kính r:      Xác định ảnh O′ của tâm O. Vẽ đường tròn tâm O′, bán kính r. 

CHÚ Ý 

Nếu u ⃗ có giá song song hoặc trùng với d thì phép tịnh tiến T_u ⃗ biến d thành chính nó, kí hiệu T_u ⃗(d)=d. 

Ví dụ 3. Trong mặt phẳng toạ độ Oxy, cho vecto v ⃗=(1;2). Tìm ảnh qua phép tịnh tiến T_v ⃗, của 

1. a) điểm A(2; 3);
2. b) đường thẳng d: x−y−5=0.

Giải: 

1. a) Đặt A^′(x^′;y^′)=T_v ⃗(A).

Ta có (AA′) ⃗=v ⃗ nên {█(x^′−2=1@y^′−3=2)┤ suy ra {█(x^′=3@y^′=5)┤  

Vậy A^′(3;5). 

1. b) Lấy điểm M(5; 0) thuộc d. Gọi M′(x′; y′) và d′ lần lượt là ảnh của M và d qua T_v ⃗.

Ta có (MM′) ⃗=v ⃗ nên {█(x^′−5=1@y^′−0=2)┤ suy ra {█(x^′=6@y^′=2)┤  

Vậy M′(6; 2). 

Ta có d′ là đường thẳng đi qua M′ và có cùng vectơ pháp tuyến với d, suy ra d′ có phương trình (x –6)−(y−2)=0 hay x−y−4=0. 

Ví dụ 4. Cho đường tròn (O; R) có tâm O, bán kính R. Cho hai điểm A, B cố định sao cho đường thẳng AB không có điểm chung với (O; R), C là điểm trên (O; R). Vẽ hình bình hành ABCD. Chứng minh rằng khi C thay đổi trên (O; R), thì điểm D nằm trên một đường tròn cố định. 

Giải: 

Do A, B cố định nên (BA) ⃗ là vectơ không đổi. Trong hình bình hành ABCD, ta có (CD) ⃗=(BA) ⃗, suy ra D là ảnh của C qua phép tịnh tiến T_(BA) ⃗ Khi C thay đổi trên đường tròn (O; R) thì D nằm trên ảnh của (O; R) là đường tròn (O′;R) qua phép tịnh tiến T_(BA) ⃗. 

Thực hành 2 

Trong mặt phẳng tọa độ Oxy, xét phép tịnh tiến T_v ⃗ với v ⃗=(3;2). 

1. a) Biết ảnh của điểm M qua T_v ⃗ là điểm M’(–8; 5). Tìm tọa độ điểm M.
2. b) Tìm ảnh của đường tròn (C): (x −2)^2+(y+3)^2 =4 qua T_v ⃗.

Giải: 

1. a) Đặt M(x;y)⇒(MM^′) ⃗=(−8−x;5−y). Ta có M^′=T_v ⃗(M) ⇒ (MM^′) ⃗=v ⃗

Khi đó {█(x=−11@y=3     ) ┤  

Vậy M(−11;3). 

1. b) Đường tròn (C) có tâm I(2; −3), bán kính R=4

Gọi (C^′), I^′(x^′;y^′) lần lượt là ảnh của (C) và I qua T_v ⃗. 

⇒(C^′) có bán kính R^′=R=2 và (II^′) ⃗=(x^′−2;y^′+3) 

⇒ (II^′) ⃗=v ⃗ ⇒ {█(x^′=5   @y^′=−1)┤⇒ Tọa độ tâm I^′(5; −1) 

Vậy ảnh của đường tròn (C) là đường tròn (C^′) có phương trình là:  

(x−5)^2+(y+1)^2=4 

Vận dụng 2 

Trong Hình 8, người thợ sửa xe đã dùng kích nâng thủy lực để đưa ô tô từ mặt đất đến vị trí cần thiết thông qua phép biến hình nào? 

Giải: 

Ta thấy ô tô được nâng từ vị trí A đến vị trí B. 

Khi đó chiếc xe ô tô được tịnh tiến theo vectơ (AB) ⃗=v ⃗. 

LUYỆN TẬP 

...